2×2行列（2次正方行列）の和と積の計算（足し算とかけ算）

行と列の数が同じ行列は足したり引いたりできる。行列の足し算には交換法則や分配法則がなりたつ。行列と行列のかけ算も定義できるが交換法則はない。

2 次正方行列の足し算

\[ \left( \begin{array}{cc} 1 & 2 \\ 3 & 4 \end{array} \right) + \left( \begin{array}{cc} 100 & 200 \\ 300 & 400 \end{array} \right) = \left( \begin{array}{cc} 101 & 202 \\ 303 & 404 \end{array} \right) \]

行列の足し算は各成分をそのまま足してつくる。

\[ 101=1+100\\ 202=2+200\\ 303=3+300\\ 404=4+400 \]

もう一つ例を見てみよう。

\[ \left( \begin{array}{cc} a & b \\ c & d \end{array} \right) + \left( \begin{array}{cc} x & y \\ z & w \end{array} \right) = \left( \begin{array}{cc} a+x & b+y \\ c+z & d+w \end{array} \right) \]

引き算も同じ。

\[ \left( \begin{array}{cc} 10 & 10 \\ 10 & 10 \end{array} \right) - \left( \begin{array}{cc} 3 & 4 \\ 5 & 6 \end{array} \right) = \left( \begin{array}{cc} 7 & 6 \\ 5 & 4 \end{array} \right) \]

行列の引き算も成分を引くだけ。

行列のかけ算

\[ \left( \begin{array}{cc} 2 & 3 \\ 4 & 5 \end{array} \right) \left( \begin{array}{cc} a & b \\ c & d \end{array} \right) = \left( \begin{array}{cc} 2a+3c & 2b+3d \\ 4a+5c & 4b+5d \end{array} \right) \]

行列のかけ算は実数と同じように $\times$ の記号を省略する。行列のかけ算は前の行列の行と後の行列の列の内積を成分とする。

(1,1) 成分 ＝ 前行列 1 行目 $\cdot$ 後行列 1 列目
(1,2) 成分 ＝ 前行列 1 行目 $\cdot$ 後行列 2 列目
(2,1) 成分 ＝ 前行列 2 行目 $\cdot$ 後行列 1 列目
(2,2) 成分 ＝ 前行列 2 行目 $\cdot$ 後行列 2 列目

$\cdot$ は内積のこと。

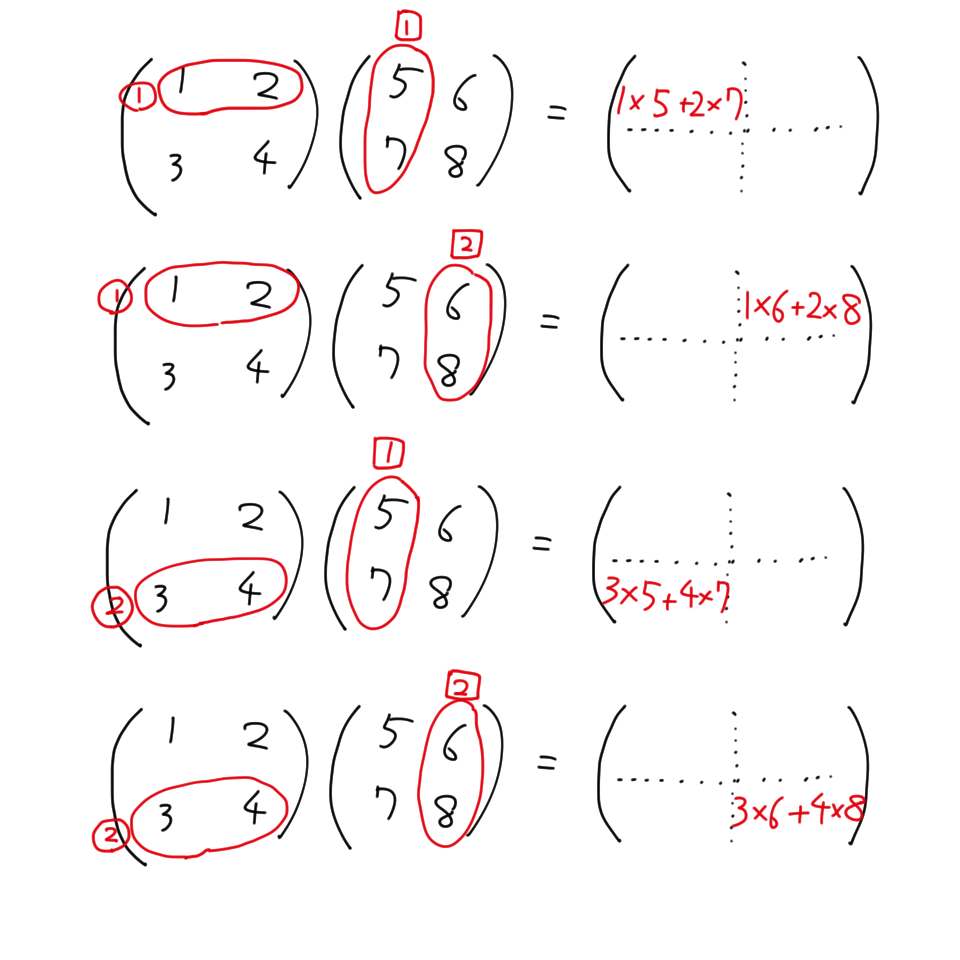
行列のかけ算は内積のくみあわせである。

行列のかけ算の確認問題

\[ (1)\ \ \left( \begin{array}{cc} 1 & -2 \\ -7 & 3 \end{array} \right) \left( \begin{array}{cc} 4 & 5 \\ -1 & -8 \end{array} \right) \]

\[ (2)\ \ \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{cc} 2 & 3 \\ 4 & 5 \end{array} \right) \]

\[ (3)\ \ \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{cc} 9 & -3 \\ -5 & 7 \end{array} \right) \]

\[ (4)\ \ \left( \begin{array}{cc} -2 & 11 \\ 4 & 8 \end{array} \right) \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \]

\[ (5)\ \ \left( \begin{array}{cc} 3 & 5 \\ 1 & 2 \end{array} \right) \left( \begin{array}{cc} 2 & -5 \\ -1 & 3 \end{array} \right) \]

解答

\[ (1)\ \ \left( \begin{array}{cc} 1 & -2 \\ -7 & 3 \end{array} \right) \left( \begin{array}{cc} 4 & 5 \\ -1 & -8 \end{array} \right)\\ = \left( \begin{array}{cc} 1\cdot 4+(-2)\cdot(-1) & 1\cdot 5+(-2)\cdot(-8) \\ (-7)\cdot 4+3\cdot(-1) & (-7)\cdot 5+3\cdot(-8) \end{array} \right)\\ = \left( \begin{array}{cc} 6 & 21 \\ -31 & -59 \end{array} \right) \]

\[ (2)\ \ \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{cc} 2 & 3 \\ 4 & 5 \end{array} \right) = \left( \begin{array}{cc} 2 & 3 \\ 4 & 5 \end{array} \right) \]

\[ (3)\ \ \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{cc} 9 & -3 \\ -5 & 7 \end{array} \right) = \left( \begin{array}{cc} 9 & -3 \\ -5 & 7 \end{array} \right) \]

\[ (4)\ \ \left( \begin{array}{cc} -2 & 11 \\ 4 & 8 \end{array} \right) \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) = \left( \begin{array}{cc} -2 & 11 \\ 4 & 8 \end{array} \right) \]

\[ (5)\ \ \left( \begin{array}{cc} 3 & 5 \\ 1 & 2 \end{array} \right) \left( \begin{array}{cc} 2 & -5 \\ -1 & 3 \end{array} \right) = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \]

行列のかけ算と単位行列

\[ I= \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \]

行列 $I$ を単位行列という。単位行列と任意の行列の積はその行列になる。

\[ AI=IA=A \]

単位行列は実数の 1 と似ている。

行列のかけ算と逆行列

確認問題の最後の問題を見ると、違う行列をかけた積が単位行列になっている。

\[ AB=I \]

$B$ を $A$ の逆行列、または $A$ を $B$ の逆行列という。逆行列は実数の割り算や分数に近く、わかりやすく言うと

\[ B=\dfrac{I}{A} \]

だが、線形代数ではマイナスのべき乗で逆行列を表現する。

\[ B=A^{-1} \]