等差数列の和（1+2+3+...100）の求め方と解説（イラストつき）

1 + 2 + 3 + 4 = 10 です。もし 1 から 100 まで足したらいくつになるでしょうか？

1 + 2 + ... + 100 = ?

1 から順番に足していく問題には公式があります。

1 + 2 + ... + ○
= (1 + ○) × ○ ÷ 2

上では 100 まで足すので

1 + 2 + ... + 100
= (1 + 100) × 100 ÷ 2
= 101 × 50
= 5050

となります。

式をひっくり返す

上のような公式が正しい理由を考えてみます。1 + 2 + ... + 100 をひっくり返すと 100 + 99 + ... + 1 です。この二つの式を組みあわせると

1 + 2 + 3 + ... + 98 + 99 + 100
100 + 99 + 98 + ... + 3 + 2 + 1

となります。この二つの式の結果は同じになるので 1 + ... + 100 は 1 + ... + 100 + 100 + ... + 1 のちょうど半分になるわけです。

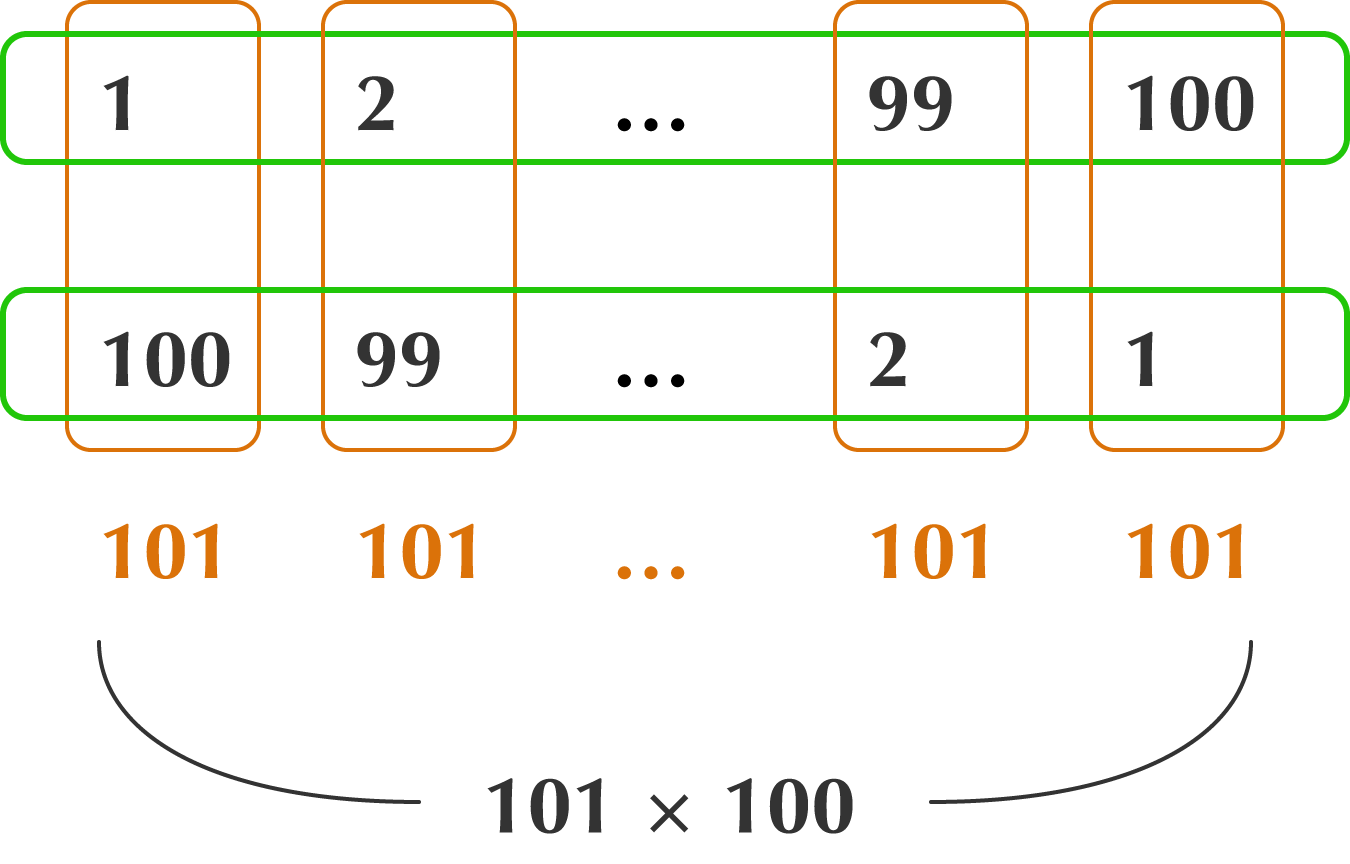
この二つの式の合計は 101 × 100 であり、それを半分にした 101 × 100 ÷ 2 が求めるものになります。

1 + ... + 100 をボールの個数と考えて、ボールを上から下に並べると

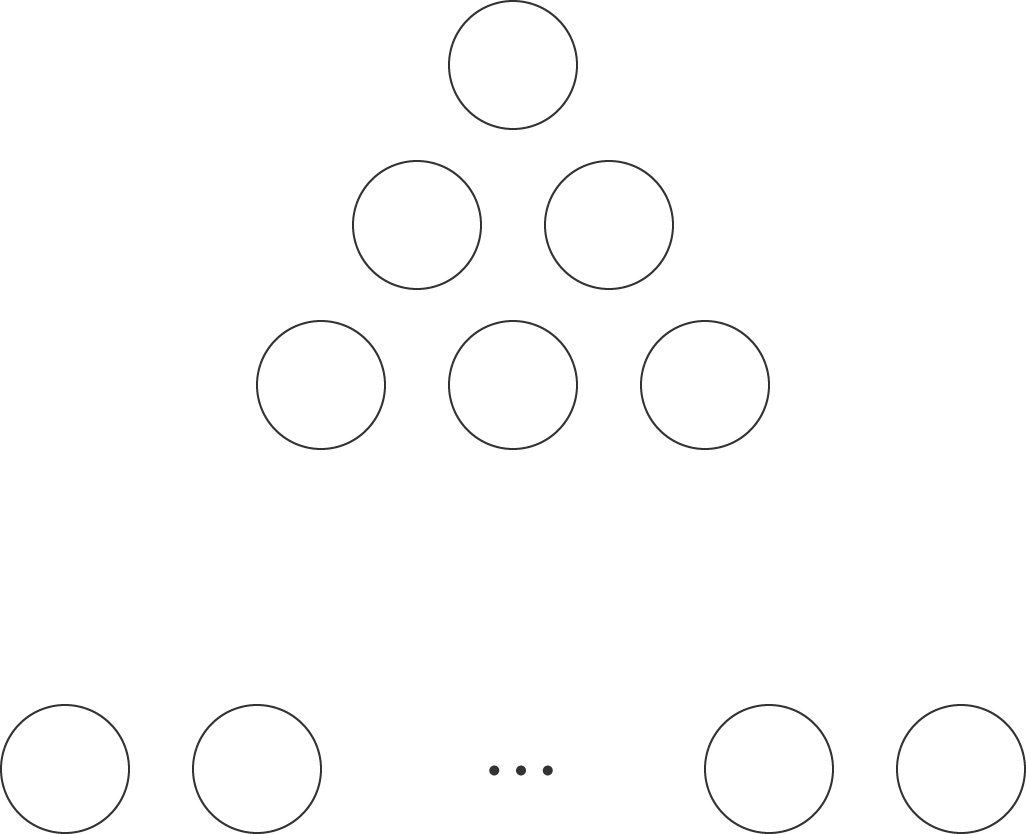
上底 1、下底 100、高さ 100 の台形になります。

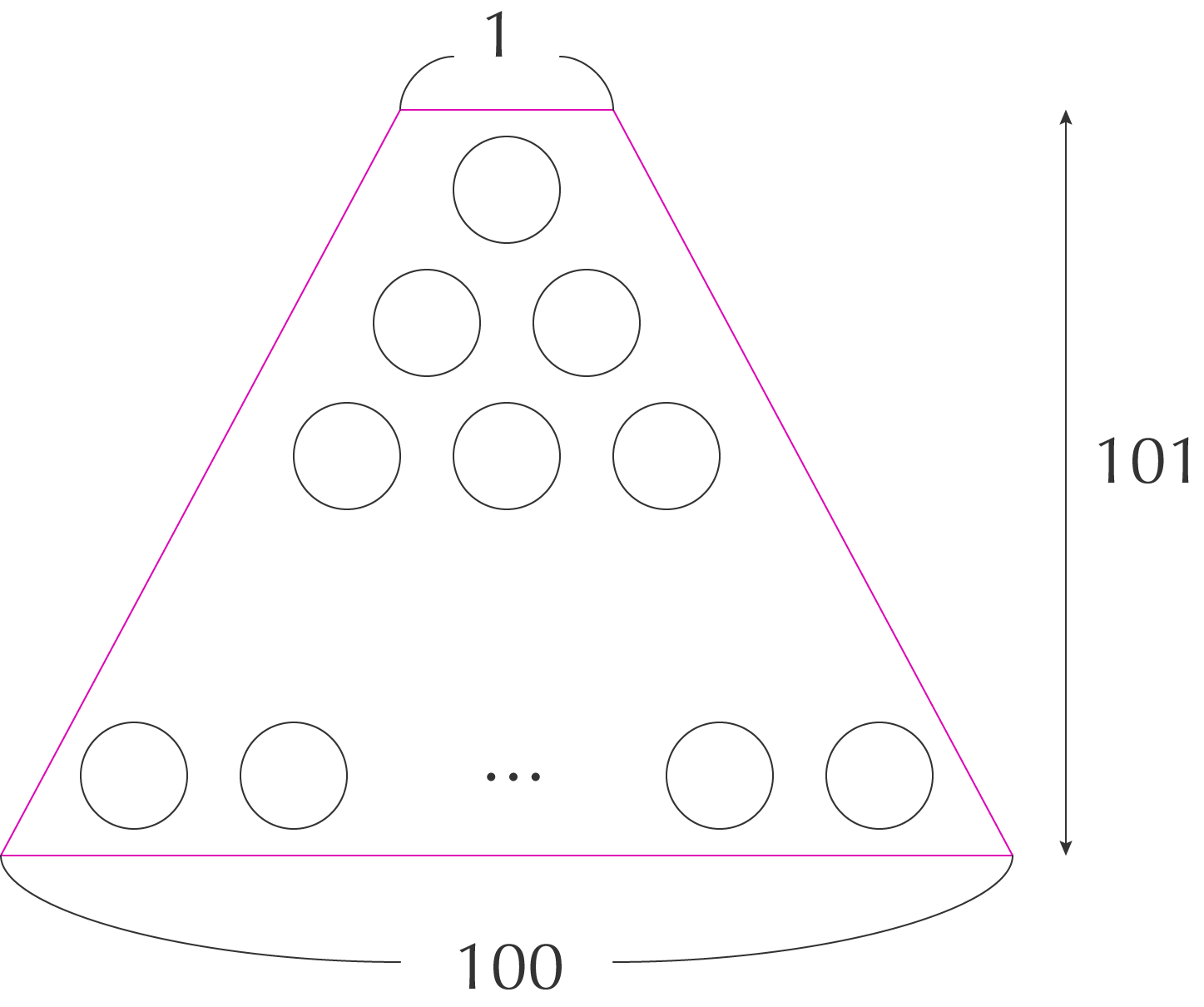
台形の面積は（上底＋下底）×高さ÷2で求められ、この面積は (1 + 100) × 100 ÷ 2 であり、公式が成りたつことがわかりました。

C言語などのプログラミングを勉強している小学生も増えているので、C言語による解法も追記します。1 + 2 + ... + 100 は次のようにプログラミングします。

#include<stdio.h>
int main() {
    int x = 0;
    for (int i = 1; i < 101; ++i)
    {
        x = x + i;
    }
    printf( "%d", x );
}

数値を表示するときは printf の第一引数を %d にします。もし 2500 まで足したいなら

#include<stdio.h>
int main() {
    int x = 0;
    for (int i = 1; i < 2501; ++i)
    {
        x = x + i;
    }
    printf( "%d", x );
}

とします。