等差数列の性質と一般項と和の公式(等差数列の和は台形の面積)
等差数列の例を見てみましょう。
$2,\ 5,\ 8,\ 11,\ \cdots,\ 95$
$2$ から $5$、$5$ から $8$ と $3$ ずつ増えています。増え方(あるいは減り方)が変わらない数列を等差数列といいます。
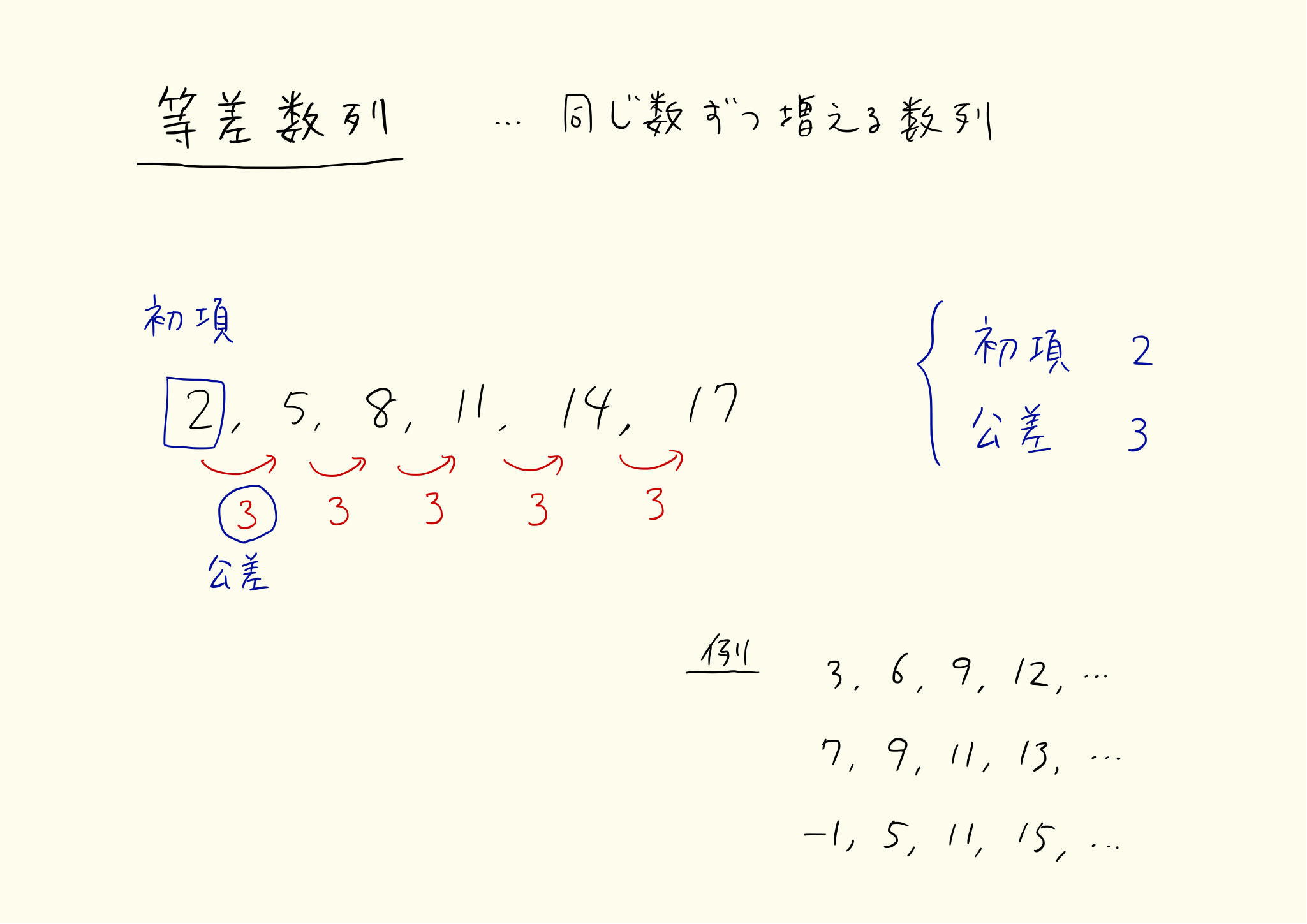
等差数列の最初の数を初項、二つの項の差を公差と呼びます。上の例では初項は2、公差は3です。
性質
上で出てきた等差数列をもう少し分析します。
2,5,8,11,14,17,20,23,26
ここで1番目と3番目の和、2番目と4番目の和、3番目と5番目の和…を求めます。
1番目と3番目の和 2+8=10
2番目と4番目の和 5+11=16
3番目と5番目の和 8+14=22
4番目と6番目の和 11+17=28
5番目と7番目の和 14+20=34
実は1番目と3番目の和は2番目の2倍、2番目と4番目の和は3番目の2倍、3番目と5番目の和は4番目の2倍となっています。
1番目と3番目の和 10=5×2
2番目と4番目の和 16=8×2
3番目と5番目の和 22=11×2
4番目と6番目の和 28=14×2
5番目と7番目の和 34=17×2
つまり等差数列では1つ飛ばしの2つの数の和は真ん中の数の2倍になっているのです。これは非常に重要な性質です。
一般項

初項a、公差dの一般項a_nは
\[ a_n=a+(n-1)d \]
となります。上の例をもう一度見てみましょう。上の等差数列の初項は2、公差は3であるため、一般項は
\[ a_n=2+(n-1)3=3n-1 \]
となりますが、この式が実際に正しいことは容易に確かめられます。3n-1のnに1,2,3,4,5を代入すると2,5,8,11,14となり、もとの数列に一致することがわかります。
和の公式
等差数列の和は台形の面積の公式と一致します。
初項a、公差d、第n項がbの等差数列において、第1項から第n項までの和S_nは
\[ S_n=\dfrac{1}{2}n(a+b) \]
となる
ここで初項を上底、末項(第n項)を下底、項数(n)を高さ、等差数列の和を台形の面積と考えてください。
初項 → 上底
末項 → 下底
項数 → 高さ
和 → 面積
とみなすと上の公式が台形の面積そのままであることがわかります。
数列(数学B)

-

-

-

-
 漸化式の公式と解き方|数学B(数列)
漸化式の公式と解き方|数学B(数列)0
1060
-
 漸化式の公式と解き方
漸化式の公式と解き方0
915
-

-





