長方形を回転してできるバームクーヘンの体積の求め方

長方形を軸から離して回転させるとバームクーヘンのような図形になります。

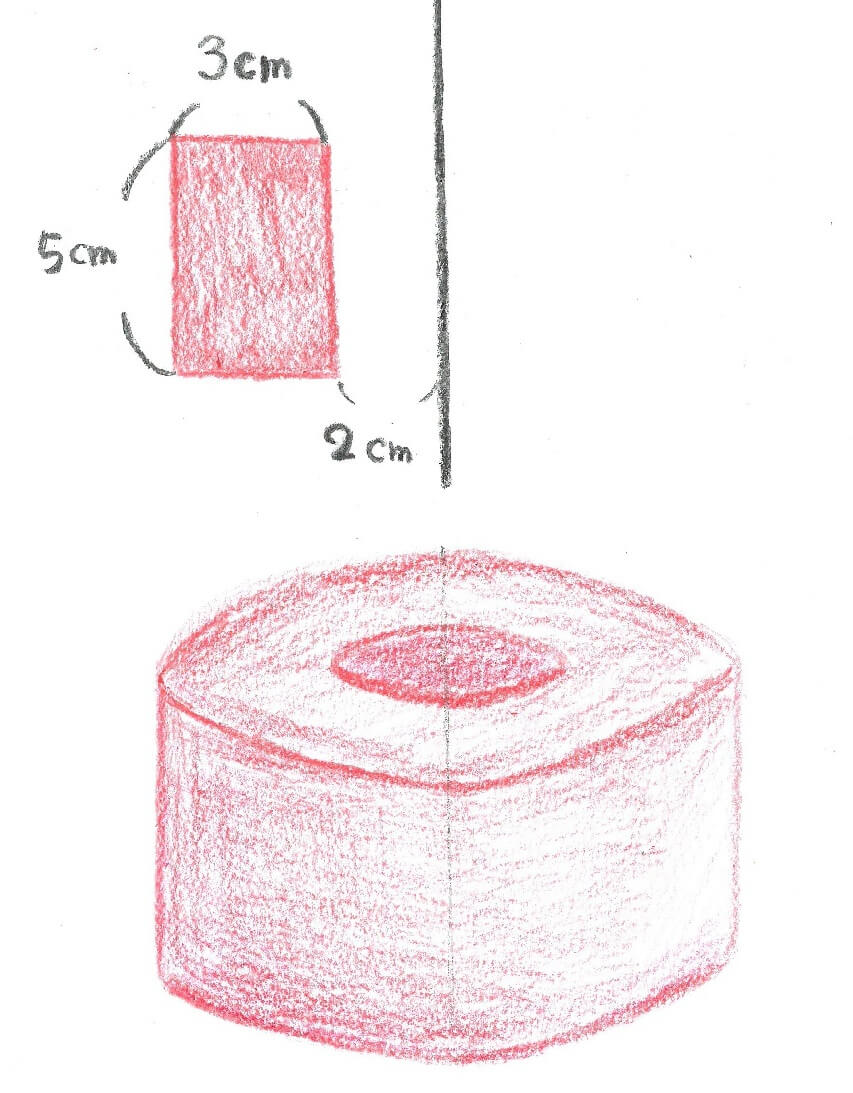
バームクーヘンは大きい円柱から小さい円柱を抜いた図形であり、体積は簡単に求まります。

バームクーヘンの体積を求める公式

(長半径×長半径-短半径×短半径)×高さ×3.14

上図では、長半径、短半径、高さはこうなります。

長半径 = 3 + 2 = 5cm
短半径 = 2cm
高さ = 5cm

長半径とは、軸と「軸から一番離れた長方形の辺」の距離のこと。短半径とは、軸と「軸から一番近い長方形の辺」の距離のこと。高さは長方形の高さです。

バームクーヘンの体積を公式にしたがって求めると

(25 - 4) × 5 × 3.14 = 329.7

となります。バームクーヘンの体積は 329.7cm² です。

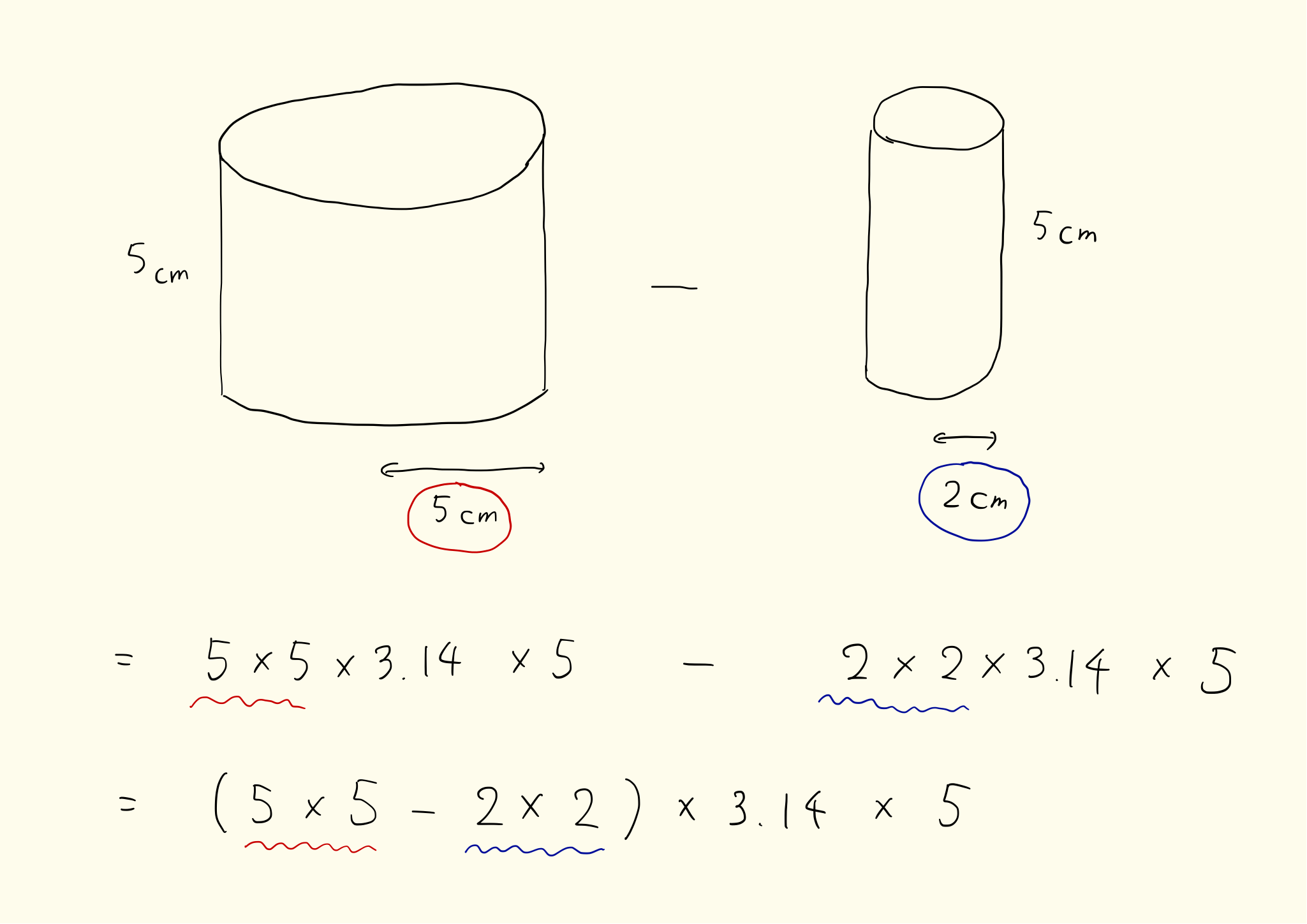
大きい円柱から小さい円柱を引いても同じ結果になる。