複素数の絶対値の定義と公式

複素数には絶対値という概念があります。複素数z=a+biの絶対値|z|を

\[ z = \left \lvert \sqrt{ a^2 + b^2 } \right \rvert \]

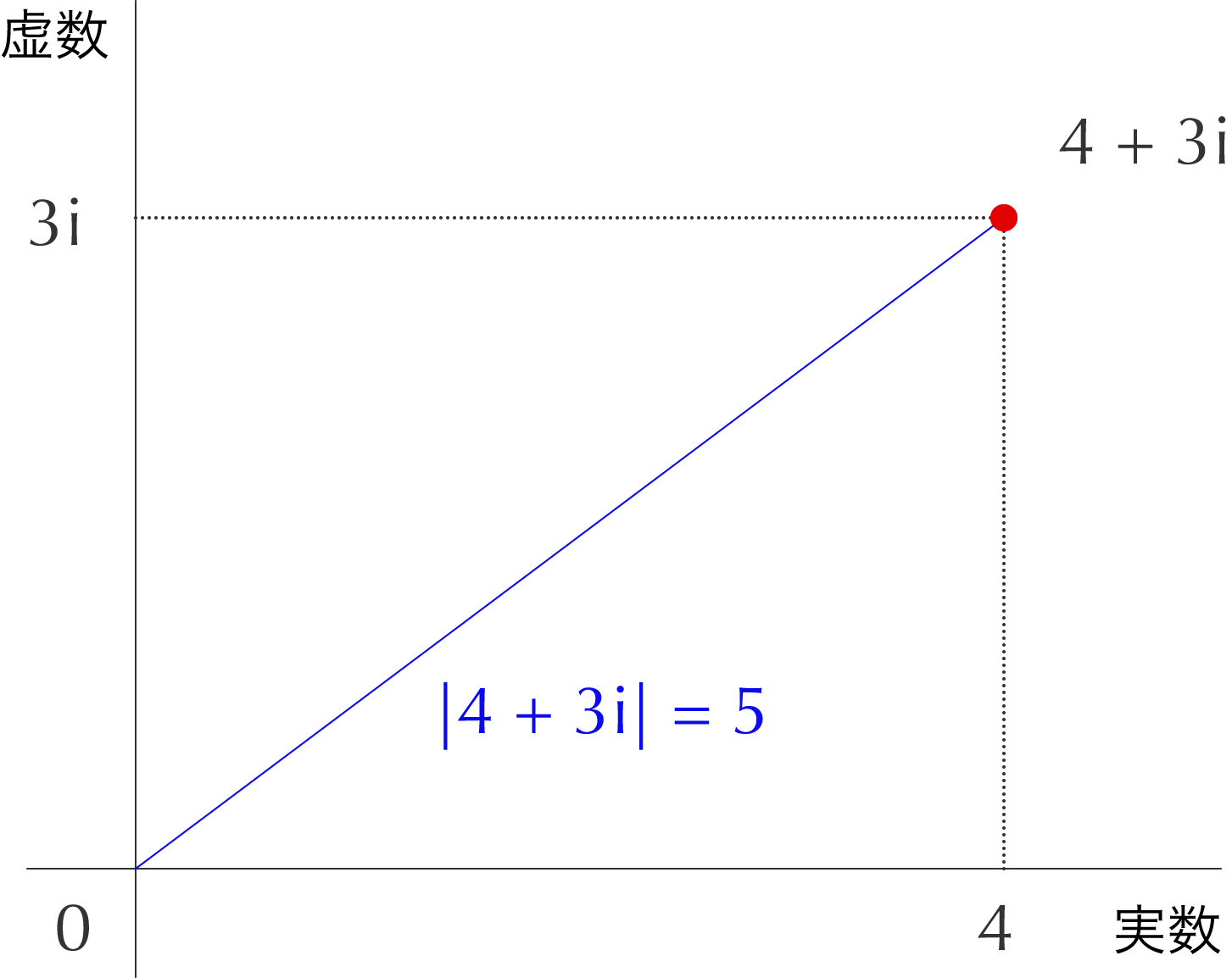
とします。これは複素数平面における複素数と原点の距離を表します。

問題

複素数の絶対値を求めなさい。

\[ (1) \quad \lvert 3+4i \rvert \\ (2) \quad \lvert 5-12i \rvert \\ (3) \quad \lvert -2+i \rvert \\ (4) \quad \lvert -3-5i \rvert \\ (5) \quad \lvert 9 \rvert \\ (6) \quad \lvert -3 \rvert \\ (7) \quad \lvert 7i \rvert \\ (8) \quad \lvert -8i \rvert \]

解答

\[ (1) \quad \lvert 3+4i \rvert = \sqrt{ 3^2 + 4^2 } = 5 \\ (2) \quad \lvert 5-12i \rvert = \sqrt{ 5^2 + (-12)^2 } = 13 \\ (3) \quad \lvert -2+i \rvert =\sqrt{ (-2)^2 + 1^2 } = \sqrt{5} \\ (4) \quad \lvert -3-5i \rvert =\sqrt{ (-3)^2 + (-5)^2 } = \sqrt{34} \\ (5) \quad \lvert 9 \rvert = 9 \\ (6) \quad \lvert -3 \rvert = 3 \\ (7) \quad \lvert 7i \rvert = 7 \\ (8) \quad \lvert -8i \rvert = 8 \]

練習問題から次の性質がわかります。

1. 複素数の絶対値は、その複素数が実数の場合、実数の絶対値に等しい
2. 純虚数の絶対値は、その純虚数からiをとった実数の絶対値になる