具体例とベン図で理解するド・モルガンの法則｜高校数学Ⅰ数と式（集合）

ド・モルガンの法則

$A,\ B$ を $U$ の部分集合とする。

\[ (1)\ \ \overline{A \cup B}=\overline{A} \cap \overline{B} \\ (2)\ \ \overline{A \cap B}=\overline{A} \cup \overline{B} \]

この2つをド・モルガンの法則という。

$A$ が $U$ の部分集合であるとは $A$ に含まれるものがすべて $U$ にも含まれていること。

ド・モルガンの法則の例

\[ U=\{1,\ 2,\ 3,\ 4\} \\ A=\{1,\ 2\} \\ B=\{1,\ 3\} \]

とする（ $A,\ B$ が $U$ の部分集合となっていることに注意。 $A$ に含まれるものがすべて $U$ にも含まれている）。

このとき

\[ \left\{ \begin{array}{l} A \cup B=\{1,\ 2, \ 3\} \\ \overline{A \cup B}=\{4\} \end{array} \right. \]

\[ \left\{ \begin{array}{l} \overline{A}=\{3,\ 4\} \\ \overline{B}=\{2,\ 4\} \\ \overline{A} \cap \overline{B}=\{4\} \end{array} \right. \]

\[ \therefore\ \ \overline{A \cup B}=\overline{A} \cap \overline{B} \]

となり、公式の $(1)$ が成り立っていることがわかる。また

\[ \left\{ \begin{array}{l} A \cap B=\{1\} \\ \overline{A \cap B}=\{2,\ 3,\ 4\} \end{array} \right. \]

\[ \left\{ \begin{array}{l} \overline{A}=\{3,\ 4\} \\ \overline{B}=\{2,\ 4\} \\ \overline{A} \cup \overline{B}=\{2,\ 3,\ 4\} \end{array} \right. \]

\[ \therefore\ \ \overline{A \cap B}=\overline{A} \cup \overline{B} \]

となり、公式の $(2)$ が成り立っていることがわかる。

ド・モルガンの法則とベン図

\[ U=\{1,\ 2,\ 3,\ \cdots\ 14,\ 15,\ 16\} \\ A=\{1,\ 2,\ 3,\ 6,\ 7,\ 8,\ 11,\ 12,\ 13\} \\ B=\{7,\ 8,\ 9,\ 10,\ 12,\ 13,\ 14,\ 15,\ 17,\ 18,\ ,19,\ 20\} \]

とする。図で表すと

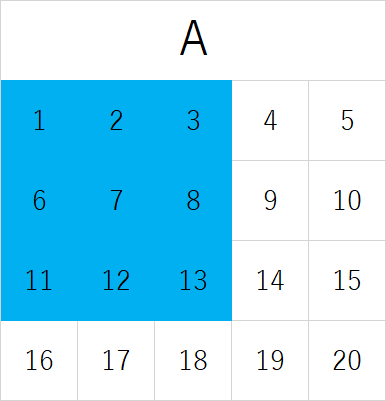
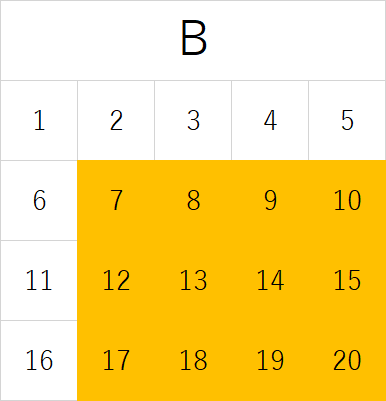
となる。

すると $A \cup B,\ \overline{A},\ \overline{B},\ \overline{A} \cap \overline{B}$ は以下のようになる。

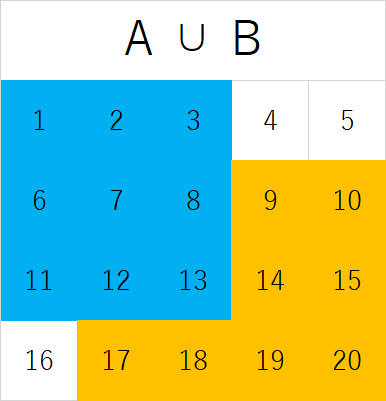
$A \cup B$ と $\overline{A} \cap \overline{B}$ の図がちょうど反転している。

これは $A \cup B$ の否定、つまり $\overline{A \cup B}$ が $\overline{A} \cap \overline{B}$ に一致することを意味する。

2つの条件の否定（ド・モルガンの法則の応用）

ド・モルガンの法則の応用として2つの条件の否定に関する法則がある。

条件の否定の法則

$p,\ q$ を条件とする。

\[ (1)\ \ \overline{p \lor q}=\overline{p} \land \overline{q} \\ (2)\ \ \overline{p \land q}=\overline{p} \lor \overline{q} \]

※ $\lor$ ：「または」、 $\land$ ：「かつ」

例えば $p$ を $x$ は $0$ より大きく、$q$ を $x$ は $10$ より小さいとしよう。すると

$p \land q$　：　$x$ は $0$ より大きく、かつ $10$ より小さい

$\overline{p \land q}$　：　$x$ は $0$ 以下か、または $10$ 以上

$\overline{p}$　：　$x$ は $0$ 以下

$\overline{q}$　：　$x$ は $10$ 以上

$\overline{p} \lor \overline{q}$　：　$x$ は $0$ 以下か、または $10$ 以上

となり、法則の $(2)$ が成り立っていることがわかる。