微分と導関数の基本(平均変化率と微分係数から公式を理解する)
微分は関数の変化率を求めるものです。変化率(特に平均変化率)とは、x がこれだけ変化したときに y はこれだけ変化するという割合をいいます。
xを時間、yを距離と考えると変化率は速度を表します。変化率が大きいとき、xが少し変化するだけでyは大きく変化します。反対に変化率が小さいとき、xが大きく変化してもyはわずかしか変化しない。
平均変化率
x が a から b まで変化したときに y がどのくらい変化したか。その変化の具合が関数の平均変化率です。下図のように、変化率は y の変化量を x の変化量で割った値です。
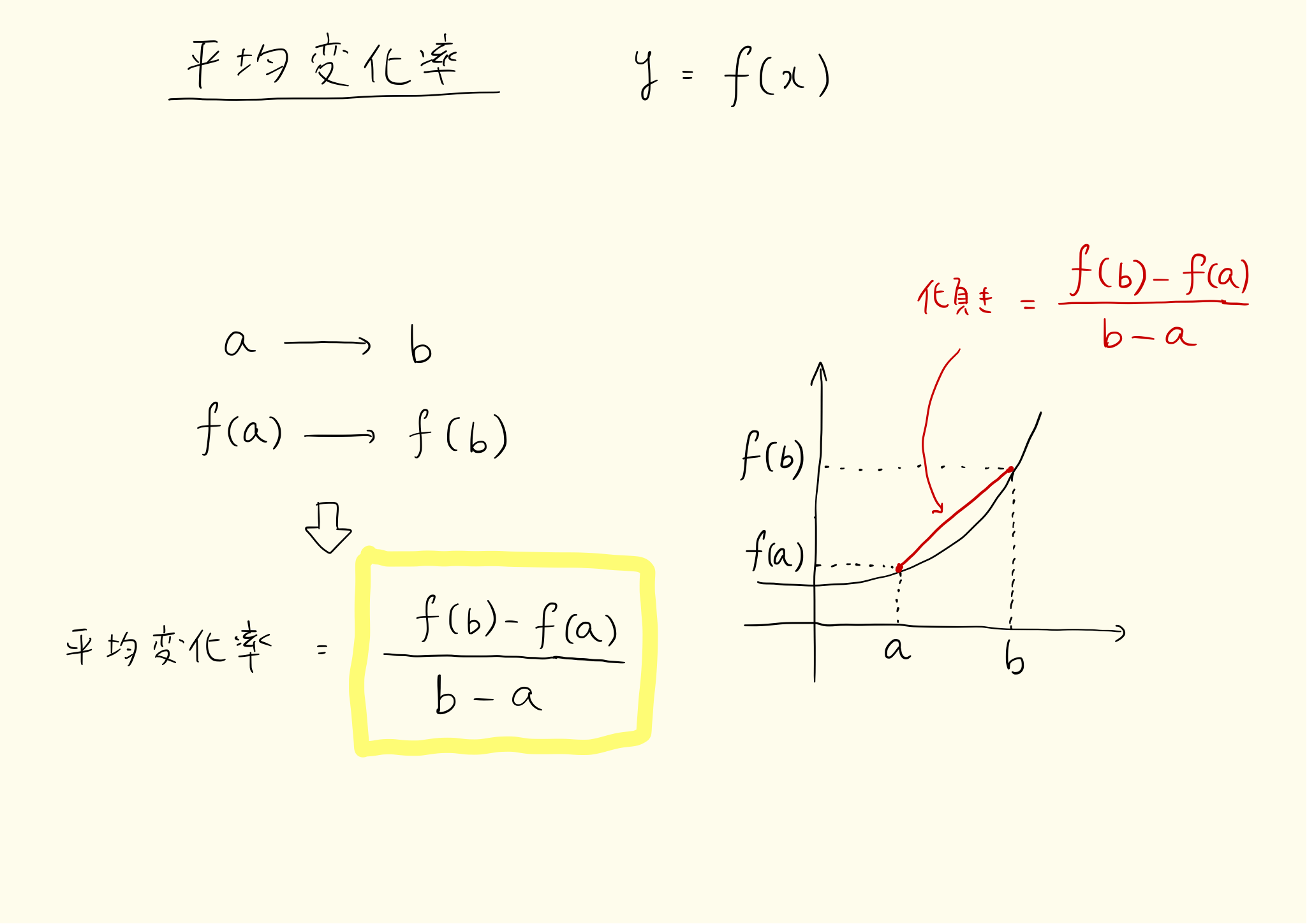
変化率そのものは簡単に求まります。x を時間、y を距離と考えると、平均変化率は平均速度そのものです。
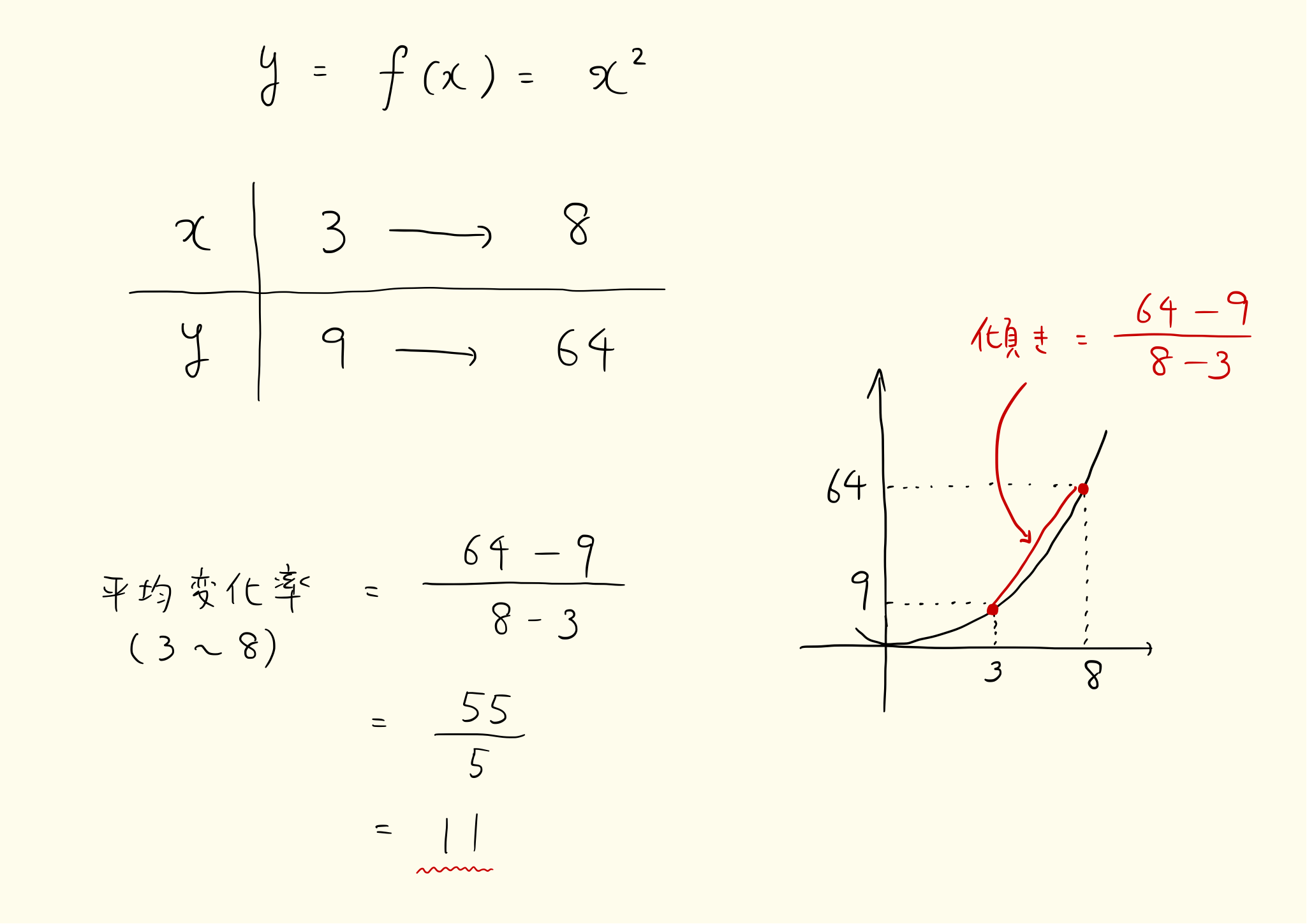
「y の変化量 ÷ x の変化量」で関数の平均変化率、すなわち平均速度がわかります。
グラフの抽象的な理解
下図のように b 点を a 点に近づけると、平均変化率は a での変化率に近づきます。
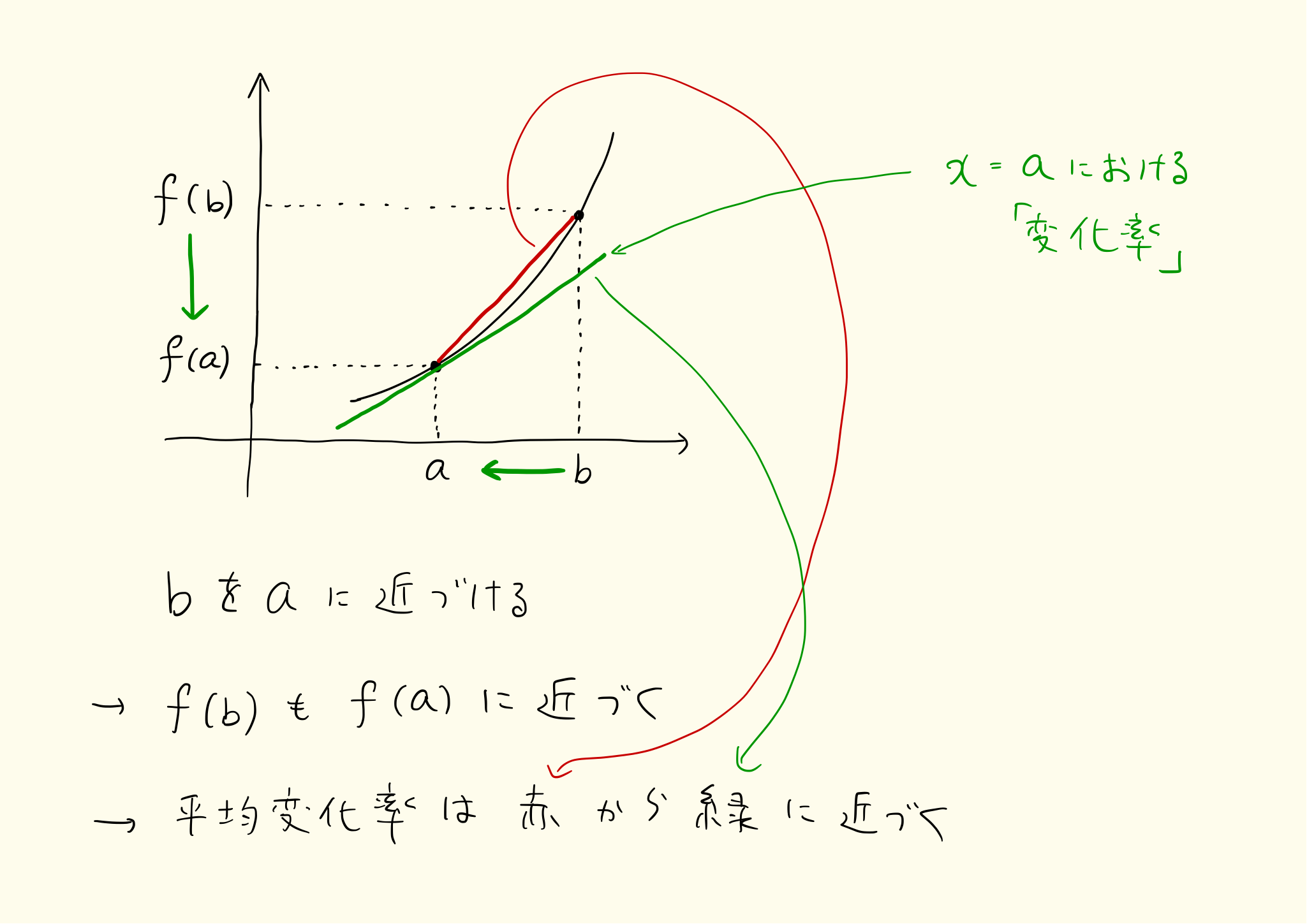
b と a が遠いと、a から b までの平均変化率はかなり大雑把な値になります。a と b の間隔を短くすれば、平均変化率の「精度」が上がって、ついには a 地点での変化率になるでしょう。
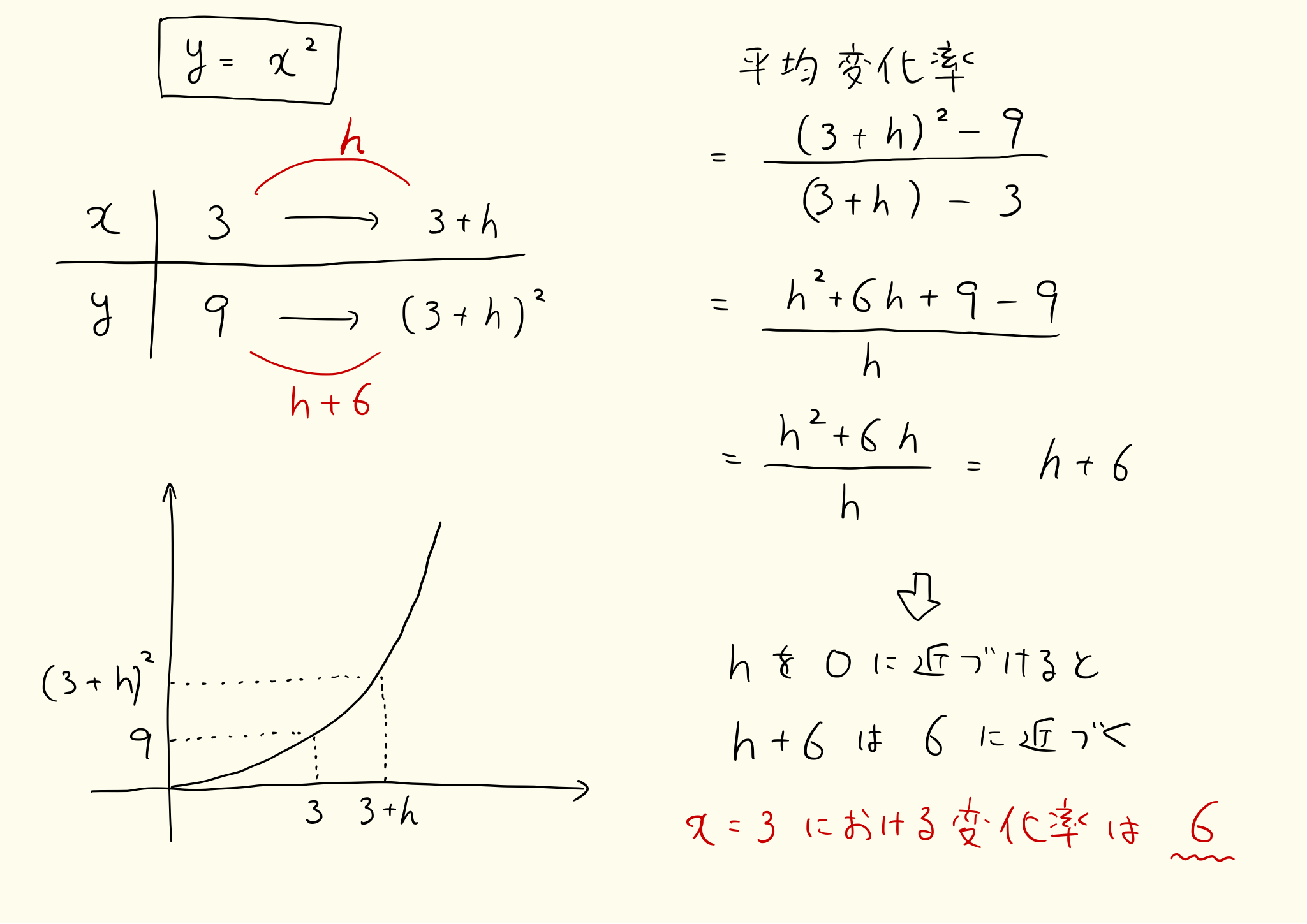
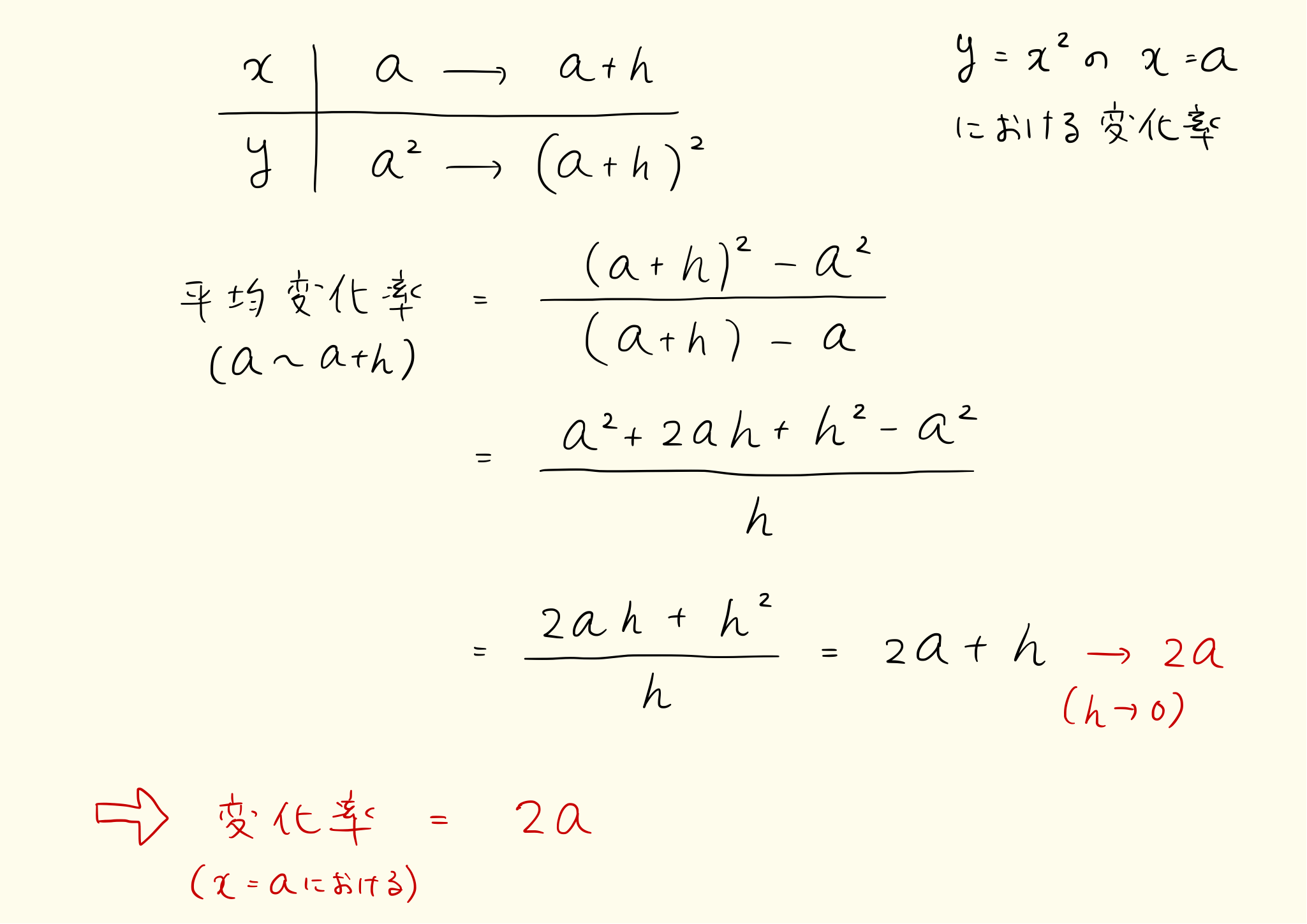
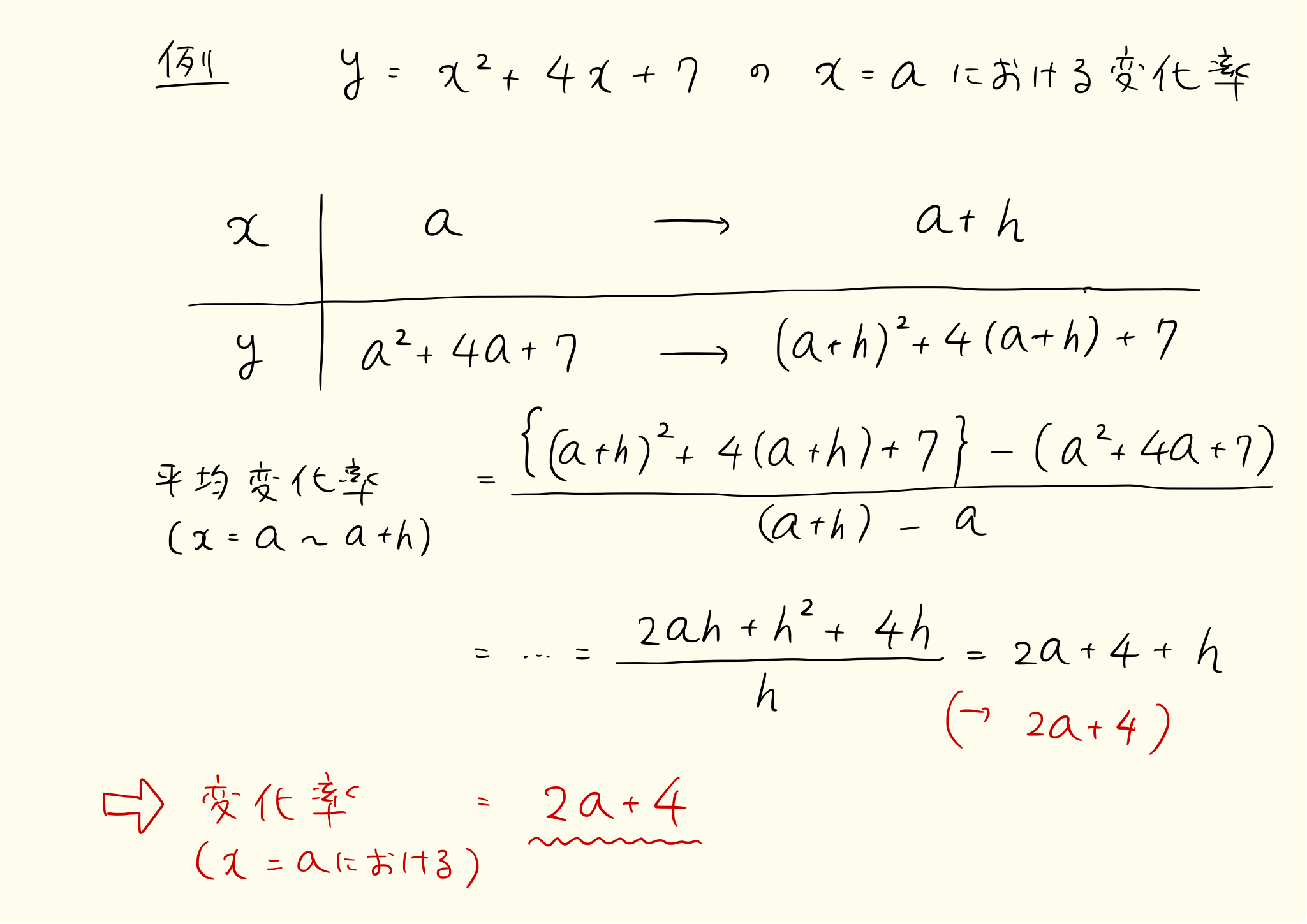
導関数


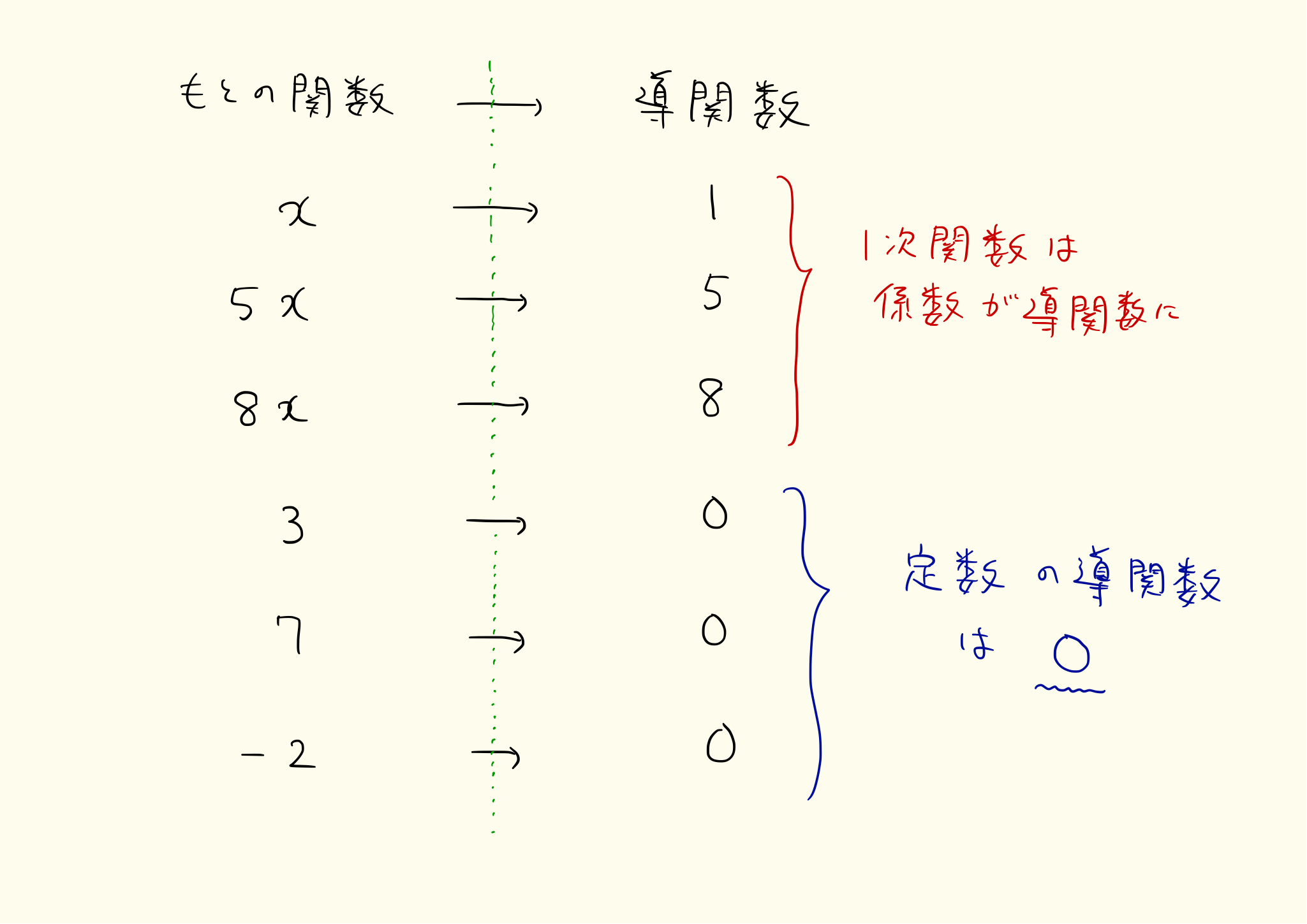


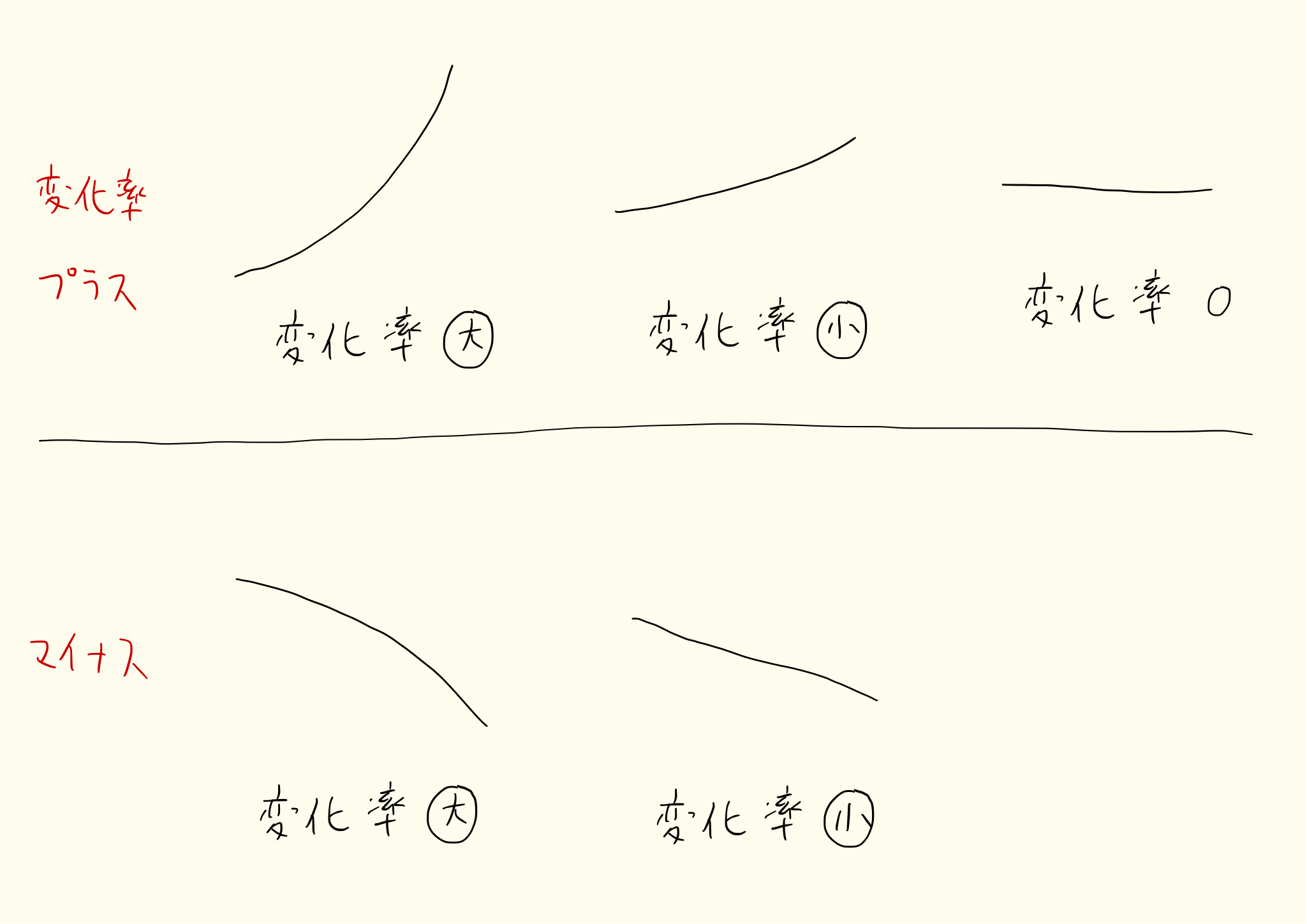
微分(数学Ⅱ)

-
 導関数の公式と微分の計算問題
導関数の公式と微分の計算問題0
1069
-
 接線と法線の方程式:解き方と問題
接線と法線の方程式:解き方と問題0
1306
-
 「微分積分って何ですか?」という質問に答えるとこうなる
「微分積分って何ですか?」という質問に答えるとこうなる0
14525
-
 微分と導関数の基本(平均変化率と微分係数から公式を理解する)
微分と導関数の基本(平均変化率と微分係数から公式を理解する)0
10219
-
 接線の方程式を計算する:微分係数の問題
接線の方程式を計算する:微分係数の問題0
86
-

-
 プラスの微分係数は関数値の増加を意味する
プラスの微分係数は関数値の増加を意味する0
123
-
 関数の増減表とグラフ - 微分の基本
関数の増減表とグラフ - 微分の基本0
83
-

-

-

-

-
 微分をざっくりわかりやすく解説
微分をざっくりわかりやすく解説0
103




