三角比の正弦定理の公式
正弦定理は三角形の辺をその対角の sin で割った値がすべて、その三角形の外接円の直径に等しくなるという定理です。
正弦定理
△ABC について $a = BC,\ b = AC,\ c = AB$ とする。また $\triangle ABC$ の外接円の半径を $R$ とする。このとき
\[ \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R \]
がなりたつ。
例題
$a = \sqrt{2},\ A = 45°,\ B = 30°$ のとき、 $b$ の値を求めなさい。
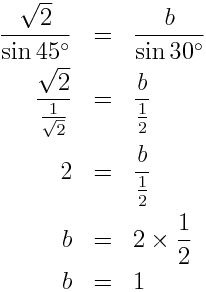
三角比(数学Ⅰ)

-
 わかりやすい三角比と基本公式
わかりやすい三角比と基本公式0
365092
-
 三角比の正弦定理の公式
三角比の正弦定理の公式0
3339
-

-





