傾きと1点の座標から1次関数を求める問題

条件から関数を求める問題は、その関数を y = ax + b として a, b を求めます。

例題

グラフの傾きが 3 で、点 (2, 5) を通る一次関数を求めなさい。

解答

求める関数を y = ax + b とすると、グラフの傾きが 3 であるから

a = 3

となり、y = 3x + b となる。またこのグラフは (2, 5) を通るから

5 = 3・2 + b
3・2 + b = 5
6 + b = 5
b = 5 - 6 = -1

となり、求める関数は y = 3x - 1 となる。

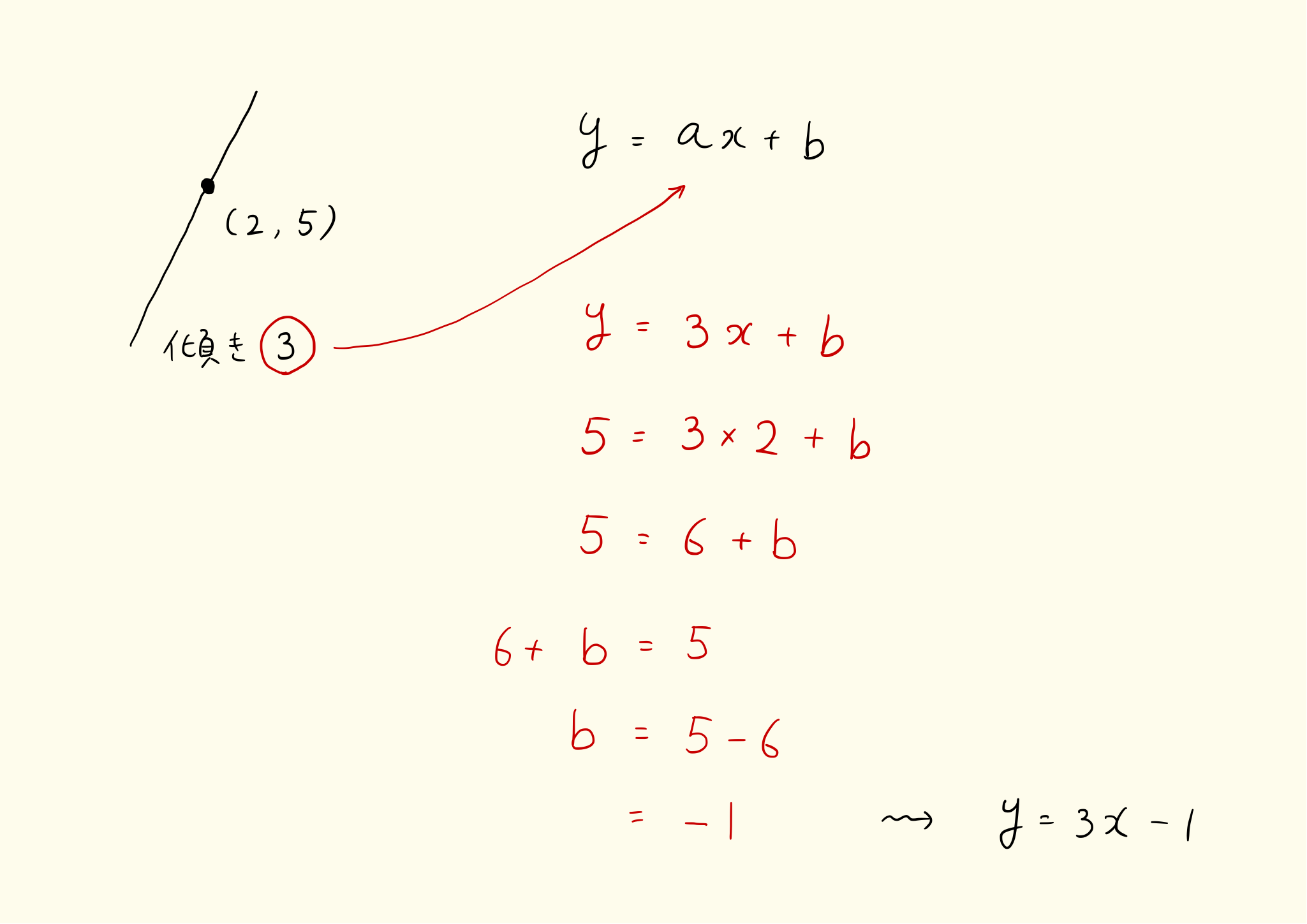
問題

次の条件を満たす一次関数を求めなさい。

(1) グラフの傾きが 4 で、点 (-1, 3) を通る。

(2) グラフの傾きが -2 で、点 (5, -6) を通る。

(3)　グラフの傾きが 0 で、点 (7, 9) を通る。

解答

(1)
求める関数を y = ax + b とすると、グラフの傾きが 4 であるから

a = 4

となり y = 4x + b となる。またこのグラフは (-1, 3) を通るから

3 = 4・(-1) + b
4・(-1) + b = 3
-4 + b = 3
b = 3 - (-4) = 7

となり y = 4x + 7 となる

(2)
求める関数を y = ax + b とすると、グラフの傾きが -2 であるから

a = -2

すなわち y = -2x + b となる。またこのグラフは (5, -6) を通るから

-6 = (-2)・5 + b
(-2)・5 + b = -6
-10 + b = -6
b = -6 - (-10) = 4

となる。

a = -2
b = 4

となり y = -2x + 4 とわかる。

(3)
求める関数を y = ax + b とすると、グラフの傾きが 0 であるから

a = 0

すなわち y = b となる。またこのグラフは (7, 9) を通るから

9 = b

となる。

a = 0
b = 9

以上から y = 9 となる。