0
5286
中学受験によく出る部分分数分解の問題と解き方
分数を「二つの分数の差」にすることを部分分数分解といいます。
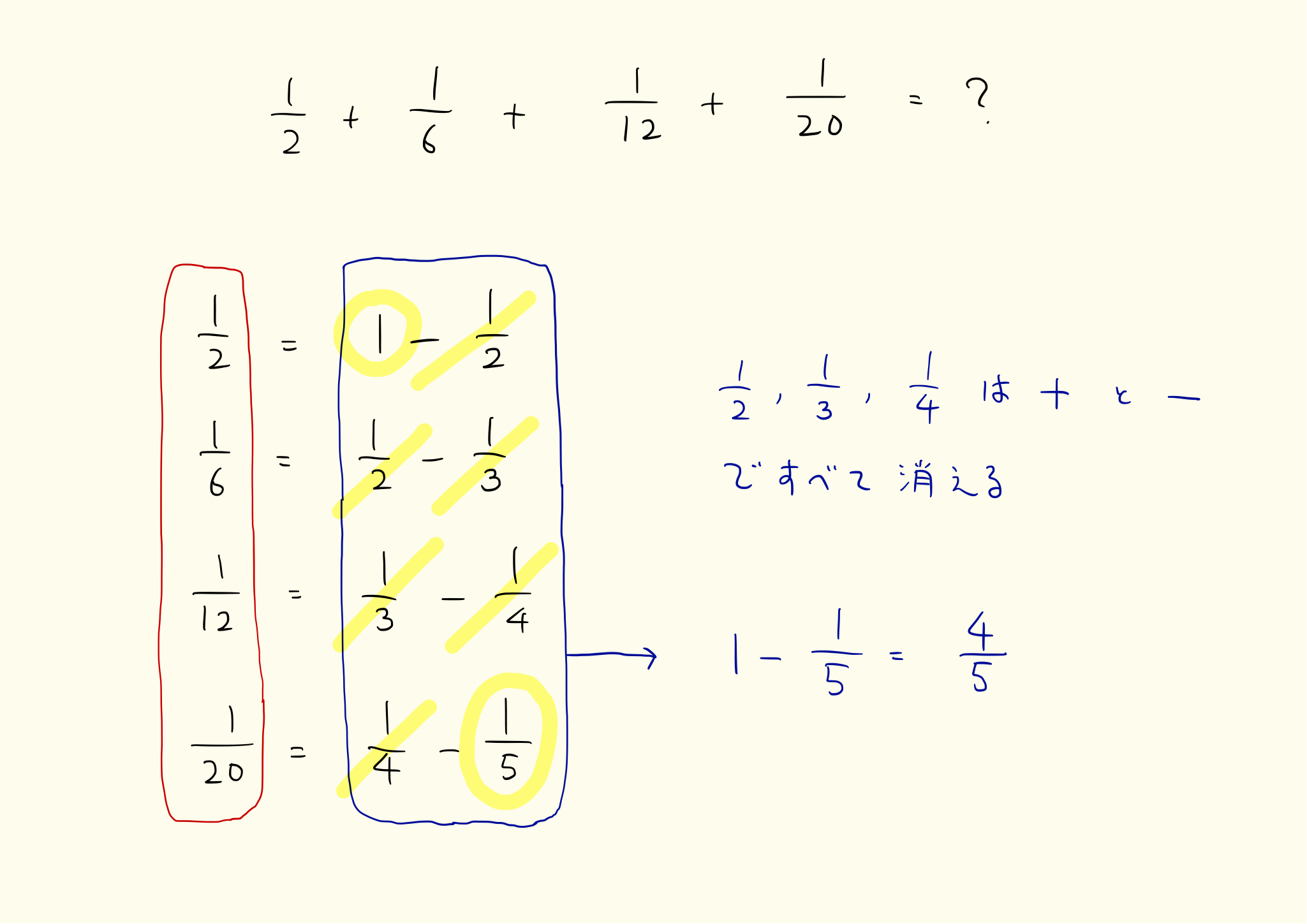
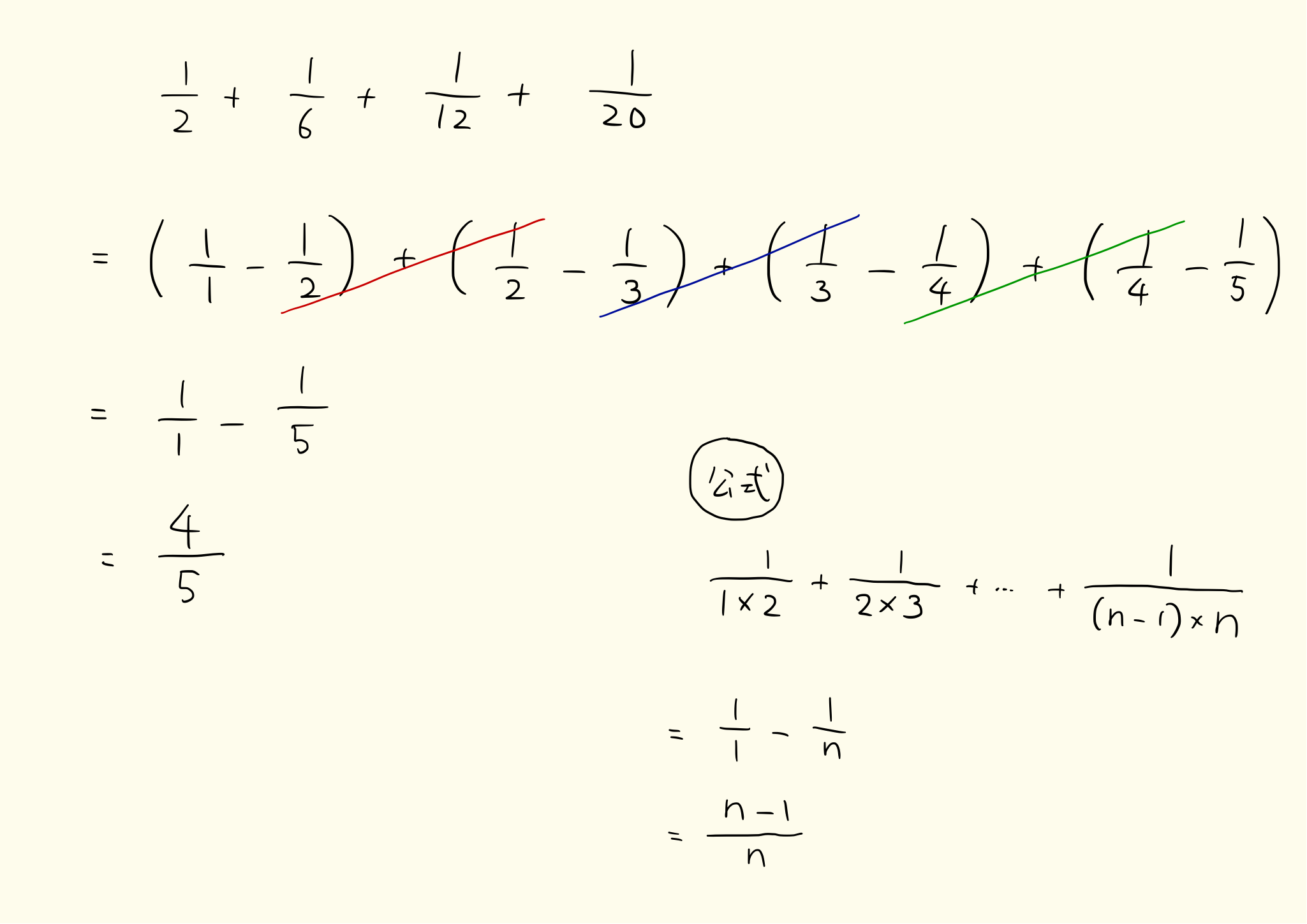
小学算数
-
立方体の表面積を求める計算と公式（辺と表面積の対応表つき）
0
15304
-
平方数一覧（1～40000）
0
46841
-
足して10になる4つの数
0
1170
-
逆数一覧（1～0.01）
0
2677
-
2進数、10進数、16進数の対応表
0
300
-
-
差集め算の基本的な問題と解き方
0
626
-
通過算の基本的な解き方
0
348
-
三角形の面積の公式はどうして底辺×高さ÷2なのか？
0
1534
-
-
-
24と36の公約数と最大公約数、最小公倍数
0
25070
-
百分率と割合の計算（○パーセントを○割○分にする問題）
0
63304
-
立体の表面積と体積の解説記事まとめ
0
1218
-
二日後は明後日？そもそも一日後は今日なのか明日なのか？
0
27489
-
約数が3個ある数は素数を2回かけた数
0
434
-
素数の定義：1はなぜ素数でないか？
0
493
-
1を7で割った循環小数に出てくる142857の性質
0
3702
-
インド式掛け算11×11から19×19までの一覧表
0
2338
-
-
-
-
三角形の図で理解する三角数
0
1090
-
長針と短針が重なる時刻と時計算
0
59842
-
中学受験によく出る部分分数分解の問題と解き方
0
5201
-
小学校で習う面積の公式まとめ
0
2642
-
多角形の対角線の本数（公式と証明）
0
2580
-
つるかめ算の面積図による解き方とポイント
0
4620
-
割合、百分率、歩合の計算問題（小学算数から中学数学まで）
0
1239
-
算数と数学の「～以上」「～以下」「～より大きい」「～未満」の違い
0
124257
-
仕事算の解き方と問題｜中学受験算数の文章題
0
1224
-
長さや重さの単位の変換
0
2879
-
円すい（円錐）の体積の求め方と問題｜小学数学
0
14079
-
帯分数を仮分数にする問題の解き方
0
4683
-
道の経路の場合の数を求める問題
0
1348
-
図で覚える多角形の外角の和の公式
0
1385
-
三角定規と角度が 150° の三角形の長さと面積を求める
0
10873
-
算数の速さの公式と基本（小学生向け）
0
1934
-
分母がちがう分数の足し算と引き算
0
205
-
かけ算の九九（一のだん）｜小学２年生・算数
0
261
-
かけ算の九九（二のだん）｜小学２年生・算数
0
336
-
百分率の解説と計算その１（小学算数）
0
554
-
小学算数・割り算の計算問題（２桁を１桁で割る計算）
0
3745
