確率の問題と解き方(さいころやくじなど)|中学数学
確率の相対度数は「ある出来事がどのくらいの頻度で起きたか」を表します。
相対度数 = 起きた回数 ÷ 試行回数
さいころを投げるゲームでは「さいころを投げる回数」が試行回数です。さいころを100回ふって1の目が32回出たら、相対度数は32/100となります。
例題
次の表は1個のさいころを投げたときの結果である。○にあてはまる数を埋めなさい。
| 投げた回数 | 2の目が出た回数 | 2の目が出る相対度数 |
|---|---|---|
| 100 | 20 | ○ |
| 200 | ○ | 3/20 |
| 300 | 52 | ○ |
| 600 | ○ | 4/25 |
解答
| 投げた回数 | 2の目が出た回数 | 2の目が出る相対度数 |
|---|---|---|
| 100 | 20 | 20/100 |
| 200 | 30 | 3/20 |
| 300 | 52 | 52/300 |
| 600 | 96 | 4/25 |
例えば96という数は
96=600×4/25
で求める。
確率の問題
確率はその出来事が起きる可能性を示すもので
確率 = その出来事の数 ÷ 全体の出来事の数
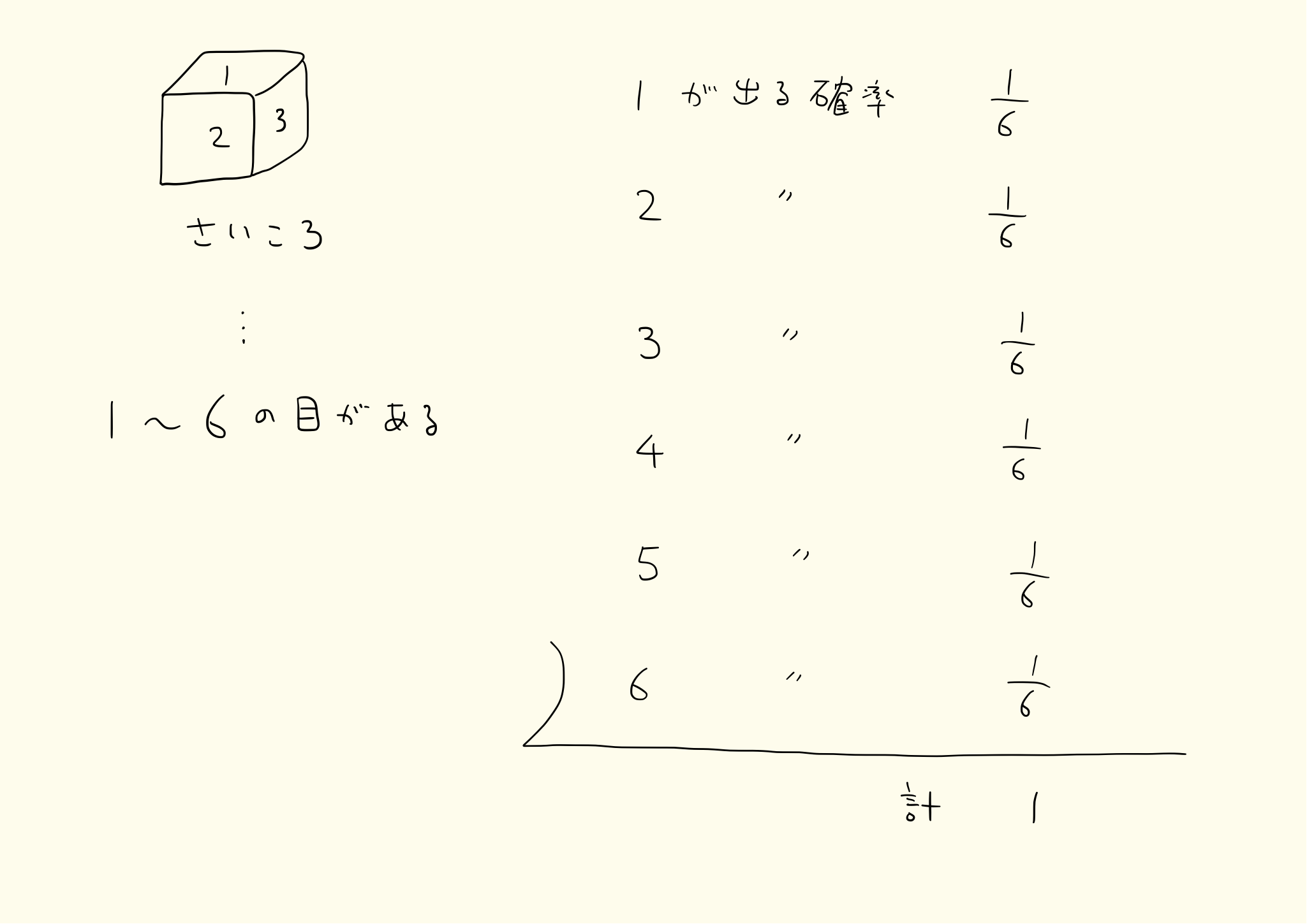
で計算します。例えばさいころをふって1が出る確率は1/6です。出来事は1通りで、全体の可能性は1〜6の6通りだからです。
1/6=1÷6
同じように2が出る確率も3が出る確率も1/6です。
10本のくじに3本の当たりが入っているとき、当たりを引く確率は
当たりの数 = 3本
全体の数 = 10本
なので3/10です。
問題
1つのさいころを投げるとき、次の確率を求めなさい。
- 2の目が出る確率
- 2または3の目が出る確率
- 5以上の目が出る確率
- 4未満の目が出る確率
解答
- 1/6
- 2/6=1/3
- 2/6=1/3
- 3/6=1/2


問題
大小2つのさいころを投げるとき、次の確率を求めなさい。
- 両方とも1の目が出る確率
- 出た目の和が3になる確率
- 出た目の和が7になる確率
- 出た目の差が5になる確率
- 出た目の差が2になる確率
解答
さいころの出方は6×6=36通りです。
(1)
両方とも1がでるパターンは(1,1)の1通りしかない。
1/36
(2)
出た目の和が3になるパターンは(1,2)か(2,1)の2通り。
2/36=1/18
(3)
出た目の和が7になるのは
(1,6)
(2,5)
(3,4)
(4,3)
(5,2)
(6,1)
の6通り。
6/36=1/6
(4)
出た目の差が5になるのは
(1,6)
(6,1)
の2通り。
2/36=1/18
(5)
出た目の差が2になるのは
(1,3) (3,1)
(2,4) (4,2)
(3,5) (5,3)
(4,6) (6,4)
の8通り。
8/36=2/9
問題
7本のうち2本のあたりが入っているくじがある。AとBの2人がA、Bの順に1本ずつくじをひく。
(1) くじのひき方は全部で何通りか
(2) AもBも当たる確率を求めなさい。
解答
(1)
7本のくじに1から7までの番号がついているとする。
例えばAが1をひいたとすると、Bは残りの2から7までをひくことになる。つまりAが1をひくときBは6通りのひき方がある。
(A,B)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(1,7)
の6通りである。同じようにAが2,3,4,5,6,7をひくときもそれぞれ6通りであるから、くじのひき方は全部で
7×6=42
42通りある。
(2)
7本のくじのうち1と2があたりとすると、AとBの両方があたりをひくということは
(A,B)
(1,2)
(2,1)
の2通りである。全体で42通りだから確率は
2/42=1/21
となる。
問題
A、B、C、Dの4人の男子とE、Fの2人の女子がいる。6人から2人を図書委員に選ぶとき、次の問いに答えなさい。
(1) 6人から2人を選ぶ選び方は全部で何通りか
(2) A、Bが選ばれる確率を求めなさい
(3) 2人とも男子である確率を求めなさい
(4) 男子から1人、女子から1人選ばれる確率を求めなさい
解答
(1)
以下の15通り。
(A,B)
(A,C)
(A,D)
(A,E)
(A,F)
(B,C)
(B,D)
(B,E)
(B,F)
(C,D)
(C,E)
(C,F)
(D,E)
(D,F)
(E,F)
(2)
全部で15通りあるから1/15となる。
(3)
(1)のリストから2人とも男子である選び方は
(A,B)
(A,C)
(A,D)
(B,C)
(B,D)
(C,D)
の6通り。よって6/15=2/5である。
(4)
男子から1人、女子から1人選ぶケースは
(A,E)
(A,F)
(B,E)
(B,F)
(C,E)
(C,F)
(D,E)
(D,F)
の8通り。よって8/15である。
中1数学

-
 中学数学 累乗の基本と計算問題(べき乗の補足説明つき)
中学数学 累乗の基本と計算問題(べき乗の補足説明つき)0
2366
-
 中学一年生 一次方程式の計算問題
中学一年生 一次方程式の計算問題0
2477
-

-

-
 中1数学まとめ(解説と問題)
中1数学まとめ(解説と問題)0
7006
-

-
 確率の問題と解き方(さいころやくじなど)|中学数学
確率の問題と解き方(さいころやくじなど)|中学数学0
6255
-
 逆比の例と計算(分数、小数、3つ以上の数の比の逆比)|中学数学
逆比の例と計算(分数、小数、3つ以上の数の比の逆比)|中学数学0
18852
-
 中学数学の方程式の文章題攻略法
中学数学の方程式の文章題攻略法0
4091
-

-
 円周の長さから円の半径と直径を計算する|オンライン電卓
円周の長さから円の半径と直径を計算する|オンライン電卓0
10459




