中３数学　図でよくわかる三平方の定理（ピタゴラスの定理）の証明と計算問題

直角三角形の辺を $a,\ b,\ c$ （斜辺が $c$ ）としたとき

\[ c^2=a^2+b^2 \]

を三平方の定理（ピタゴラスの定理）という．直角三角形に関する定理で，斜辺の二乗が残りの辺の二乗の和に等しい．

三平方の定理の証明

直角三角形の角から斜辺と垂直な直線を引いて，直角三角形を二つに分ける．すると，もとの直角三角形と新しく中にできた直角三角形が相似の関係になる．

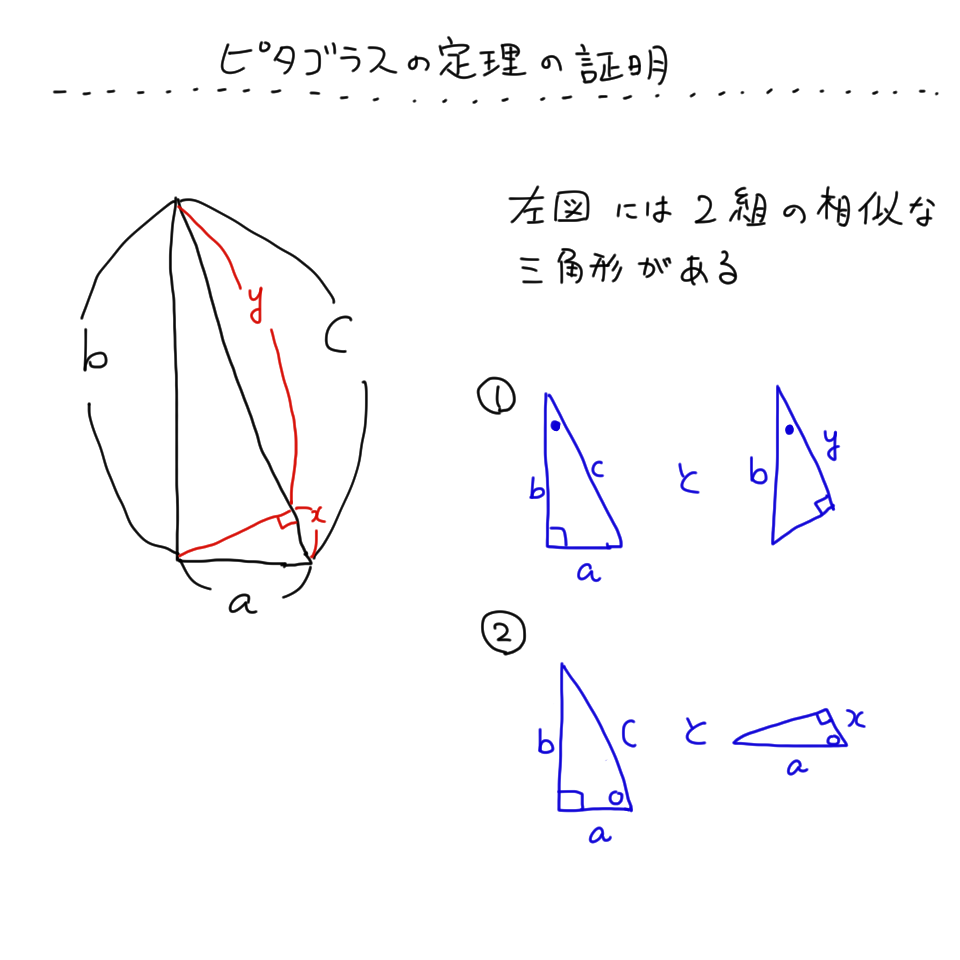
相似は二組ある．三角形の二角が一致すれば相似になることを思い出そう．

この二組の相似から

\[ c:a=a:x\\ a^2=cx \]

\[ c:b=b:y\\ b^2=cy \]

が成り立つので

\[ a^2+b^2=cx+cy=c^2 \]

となる．

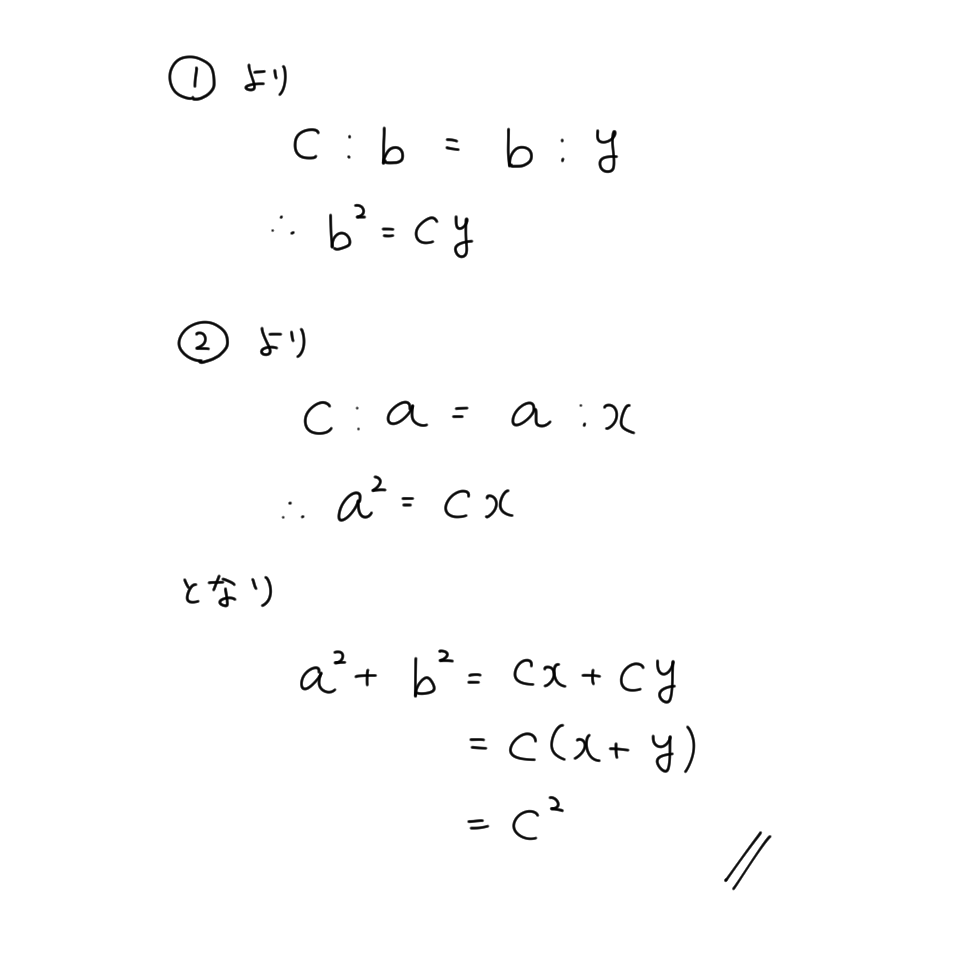
三平方の定理の証明のポイント

・直角三角形を二つの直角三角形に分けること
・二組の相似を見つけること

手書きのプリント問題

以下のプリントは三平方の定理（ピタゴラスの定理）を教えるときに使ったものです．