二次関数とグラフ|中3数学&高校数学Ⅰ
たての長さがx、よこの長さが3xの長方形の面積yを考えてみよう。

上図のように長方形の面積は3x^2です。
y=3x^2のようにx^2のある関数を2次関数といいます。y=3x^2のxにいろいろな値を入れて、yの変化を見てみましょう。
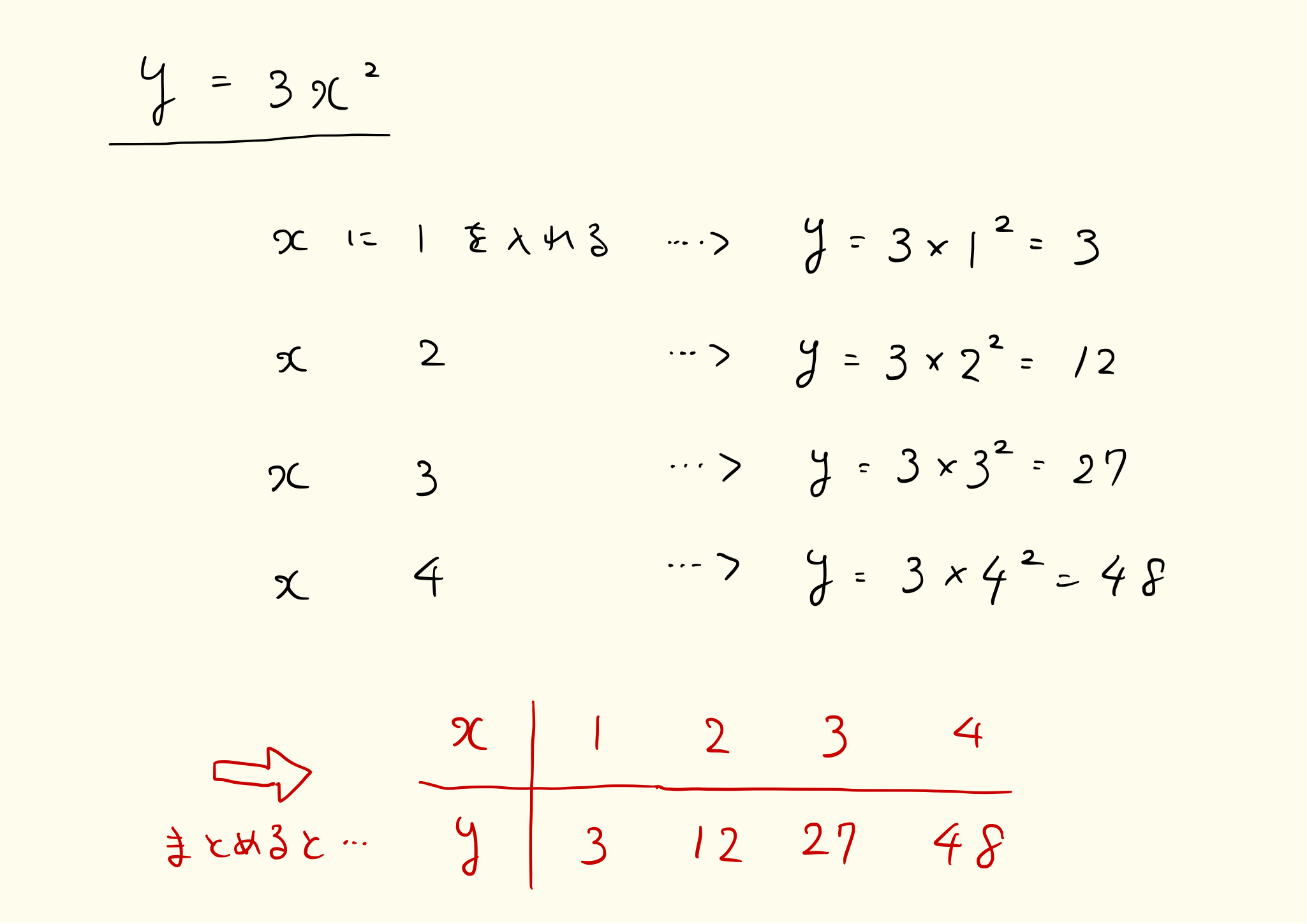
xとyの関係を表にすると、xが大きくなればなるほどyが大きくなっていることがわかります。また大きくなる度合いも大きくなっています。
| x | y |
|---|---|
| 1 | 3 |
| 2 | 12 |
| 3 | 27 |
| 4 | 48 |
二次関数(基本)
基本的な二次関数はy=ax^2で表される関数です。aは定数で、0でない実数が入ります。

y=3x^2(例題)のxに-4から4までの整数を入れてみましょう。
| x | y |
|---|---|
| -4 | 48 |
| -3 | 27 |
| -2 | 12 |
| -1 | 3 |
| 0 | 0 |
| 1 | 3 |
| 2 | 12 |
| 3 | 27 |
| 4 | 48 |
xが0より大きいとき、xが大きくなるとyも大きくなります。しかしxがマイナスのときは、xが小さくなるとyが大きくなります。またxの絶対値が等しいとき、yの値も同じになっています。
二次関数(応用)
二次関数はy=ax^2+bx+cで表される関数です。これまで扱ったy=ax^2は、y=ax^2+bx+cのbとcを0にした特殊な形です。

二次関数のグラフ
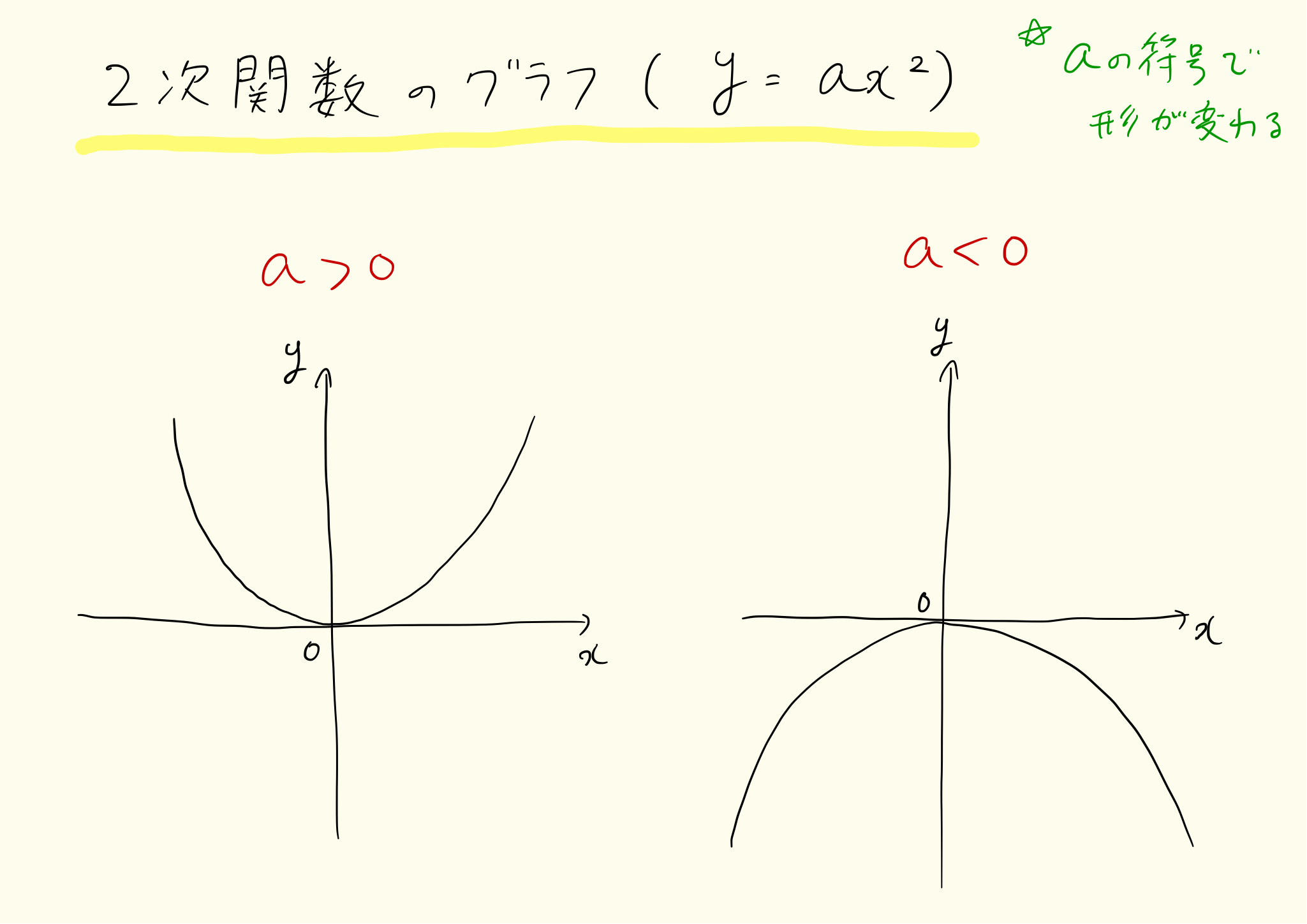
二次関数y=ax^2のグラフは下図のようにおわん型をとります。aが0より大きいとき、グラフは谷をつくります。aが0より小さいとき、グラフは山をつくります。
平行移動
二次関数は平行移動したり対称移動したりしても二次関数になります。二次関数をy=f(x)という形で表すと、このグラフをx軸方向にp、y軸方向にqだけ平行移動した関数はy-q=f(x-p)となります。
y=x^2は、x軸方向にp、y軸方向にqだけ平行移動させた関数はy-q=(x-p)^{2}となります。
平行移動してもグラフの形そのものは変わりませんが、それは上の変換で二次関数の最高次係数y=ax^{2}+bx+cでいうaが変わらないことからもわかります。平行移動によって変わるものはあくまで一次係数と定数項y=ax^{2}+bx+cでいうbとcです。
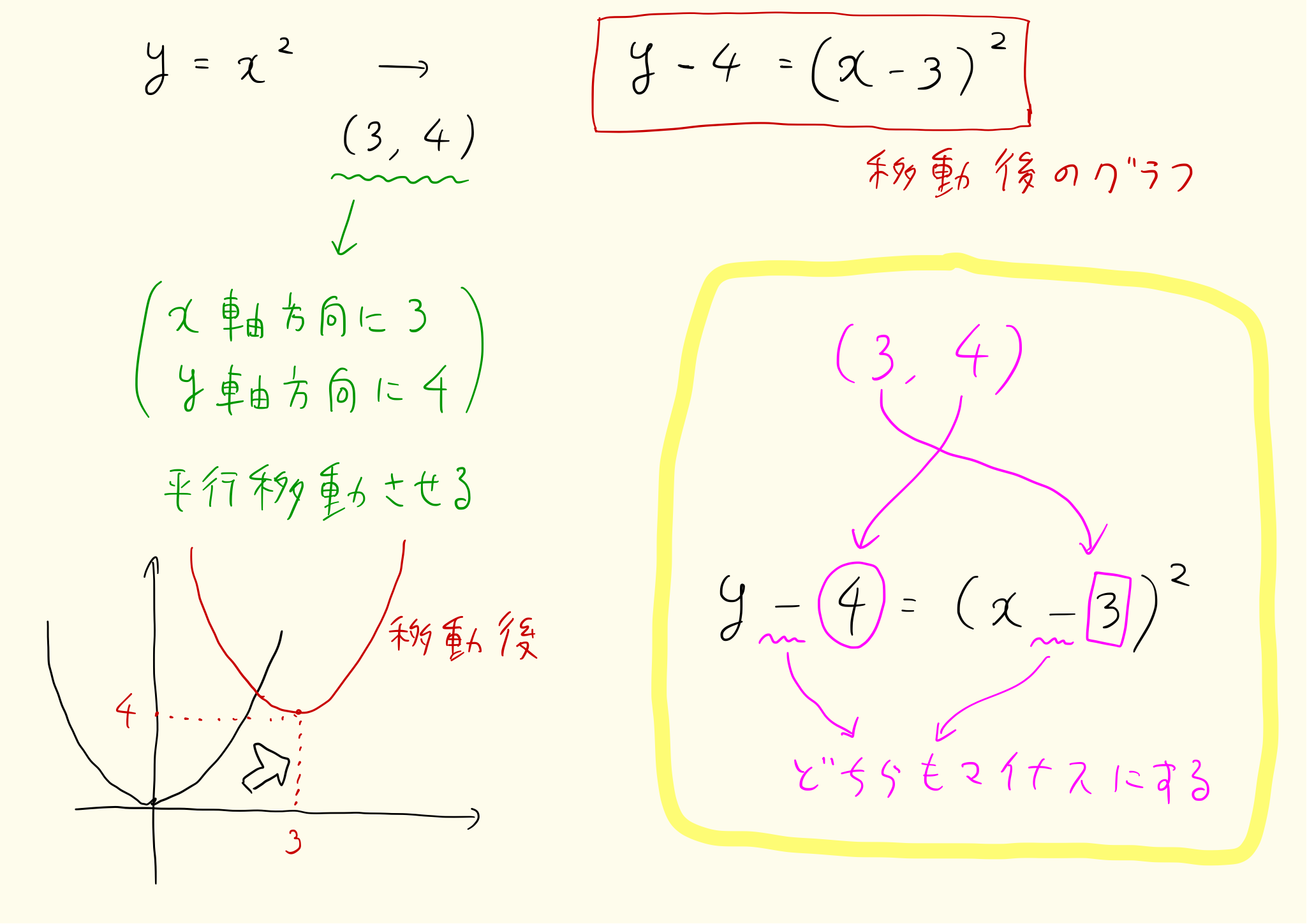
y=x^2を(3,4)だけ平行移動したグラフを上図で考えています。
二次関数(数学Ⅰ)

-
 平方完成の解き方(公式と計算問題)
平方完成の解き方(公式と計算問題)0
43307
-
 2次方程式と3次方程式の解と係数の関係
2次方程式と3次方程式の解と係数の関係0
432
-
 二次関数とグラフ|中3数学&高校数学Ⅰ
二次関数とグラフ|中3数学&高校数学Ⅰ0
1436




