平方根の性質と公式(高校数学)
9 の平方根は 3 です。平方根とは、二乗するともとの数になる数です。
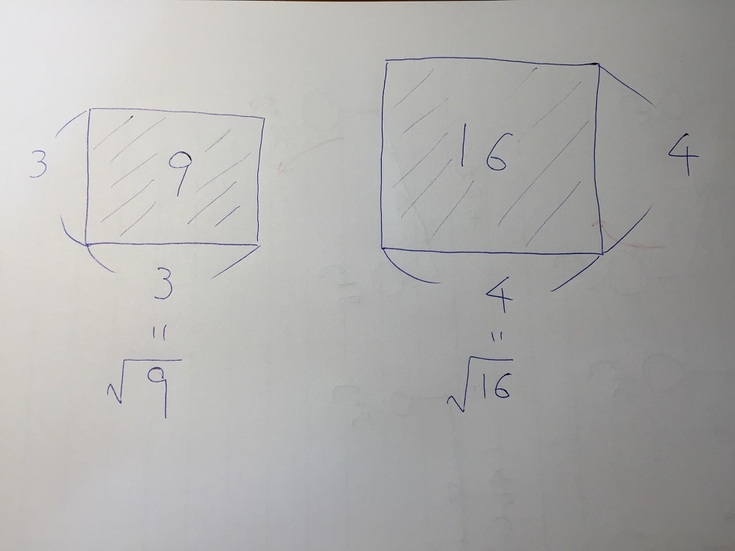
16 の平方根は 4 で、25 の平方根は 5 です。二乗すると必ず正になることから、平方根は必ず正になります。
9 や 16 の平方根は簡単な整数になりますが、7 や 11 といった一般的な数の平方根は整数になりません。
平方根の公式(応用)
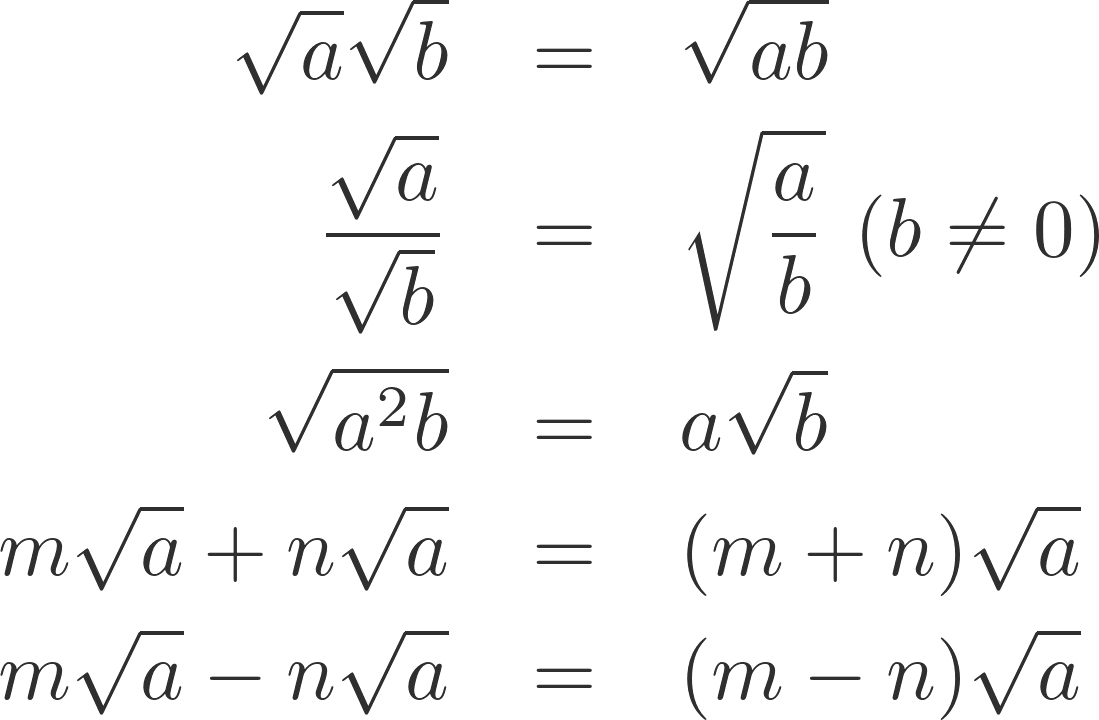
下の例題を見てわかるように、ルートの中身はなるべく小さくします。

平方根の足し算と引き算
足し算と引き算はルートの中身を同じにする。分数の足し算と引き算で分母をそろえるように、ルートの足し算と引き算でもルートの中身をそろえます。
コード
\sqrt{a}\sqrt{b}&=&\sqrt{ab}\\
\dfrac{\sqrt{a}}{\sqrt{b}}&=&\sqrt{\dfrac{a}{b}}\ (b \neq 0)\\
\sqrt{a^2 b}&=&a\sqrt{b}\\
m\sqrt{a}+n\sqrt{a}&=&(m+n)\sqrt{a}\\
m\sqrt{a}-n\sqrt{a}&=&(m-n)\sqrt{a}
根号・ルート(数学Ⅰ)

-
 ルート2、ルート3、ルート5、ルート6…の値(小数点以下30桁)と覚え方
ルート2、ルート3、ルート5、ルート6…の値(小数点以下30桁)と覚え方0
141253
-
 平方根の性質と公式(高校数学)
平方根の性質と公式(高校数学)0
5924
-
 二重根号の外し方と計算例(高校数学Ⅰ・平方根)
二重根号の外し方と計算例(高校数学Ⅰ・平方根)0
1796
-
 1から125までの立方根(小数表記)
1から125までの立方根(小数表記)0
1352
-

-

-





