単振動の公式と力学的エネルギー保存則

バネ定数 k のばねに質量 m の物体がついているとき、物質をずらして離すと振動する。バネが伸びれば縮む方向に、バネが縮めば伸びる方向に力が働く。これを弾性力という。弾性力の大きさはバネの伸び（または縮み）に比例する。

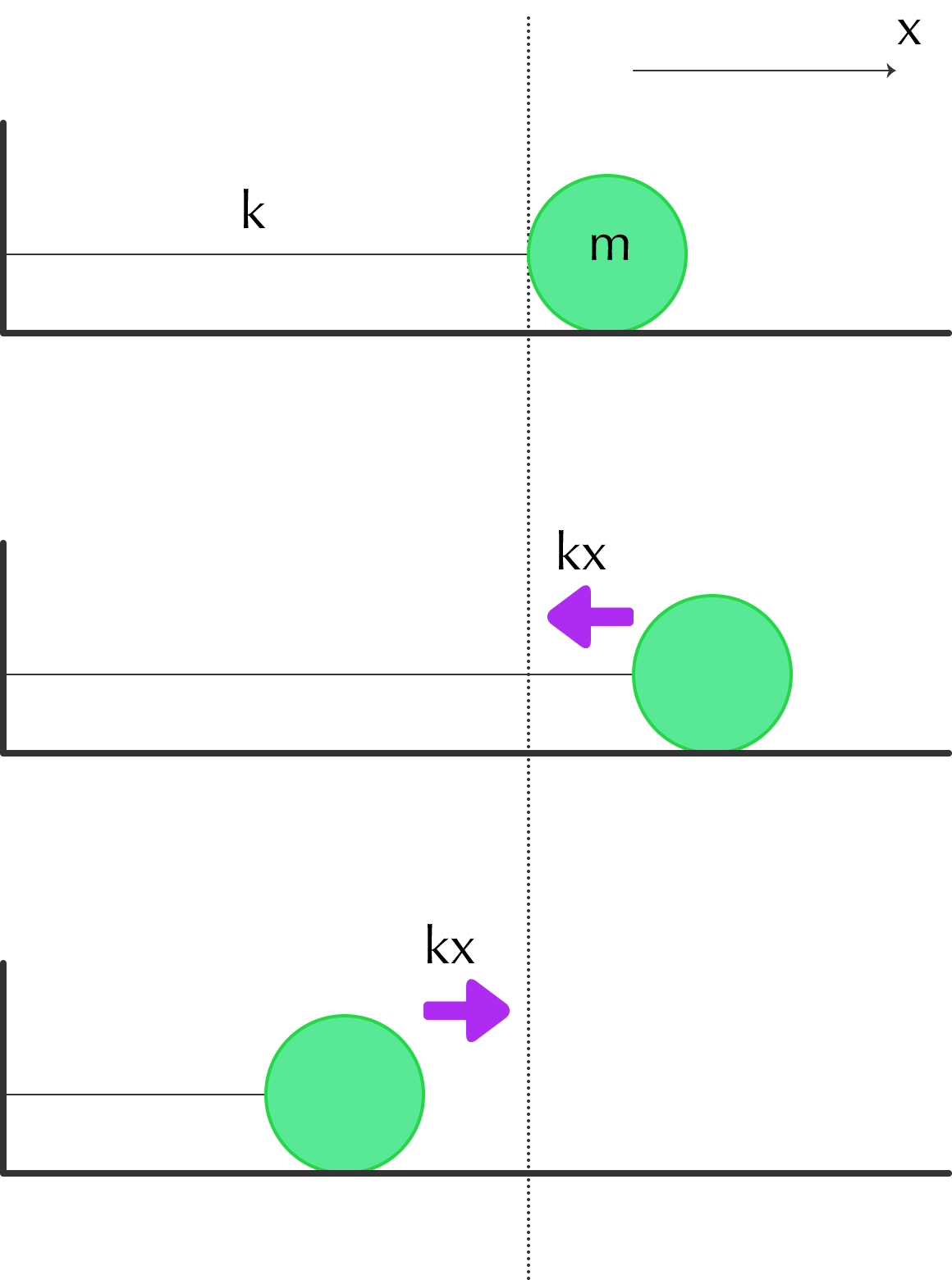
伸びる方向に x 軸をとると、バネが x 伸びたときは -kx、バネが x 縮んだときも -kx の力が働くため、バネの運動方程式は

-kx = ma

となる。ここで a は加速度である。位置と加速度（x と a）は右方向を正とすることに注意しよう。

運動方程式の解

-kx = ma の運動方程式は x = A cos ωt を解にもつ。ただし ω = √(k/m) である。

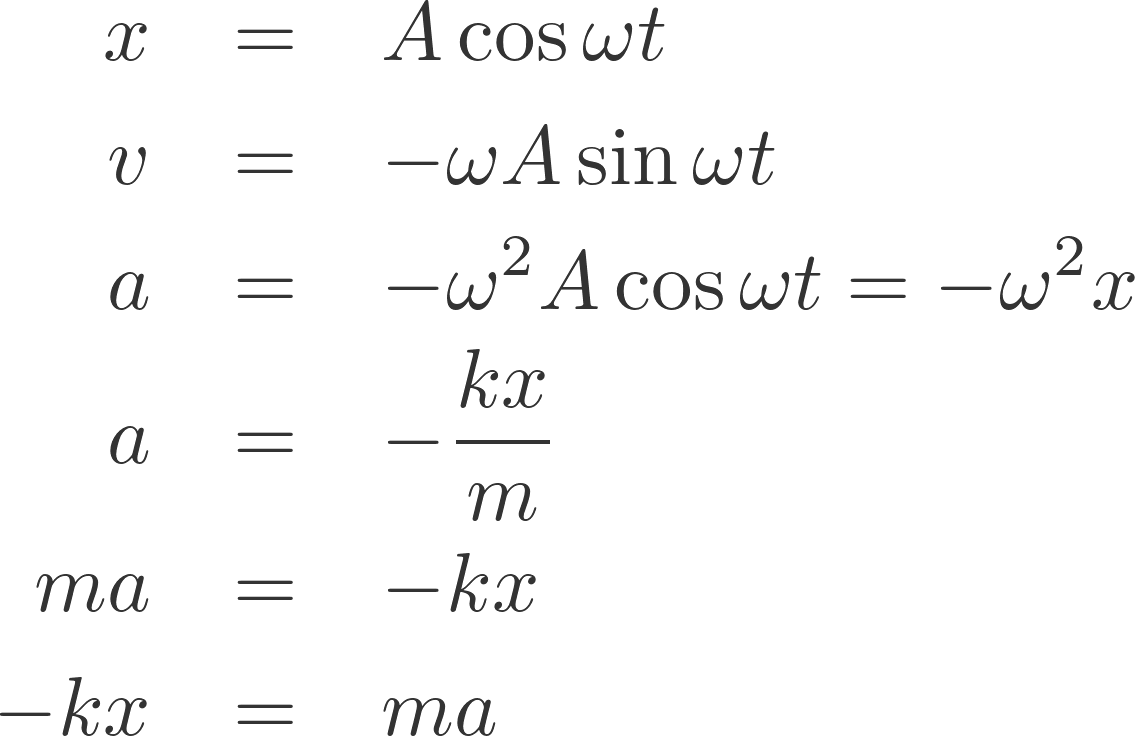
運動方程式は微分方程式（x とその微分の多項式がイコールでつながっている式）の一つであり、微分方程式の解は一つとは限らない。バネの運動方程式の解はほとんどの場合、無限にある。実際 cos についている定数の A は任意の実数である。

A はバネをずらして離したときに位置である。

cos の中身も ωt である必要はない。θ を任意の角度として x = A cos (ωt + θ) は運動方程式の解になる。

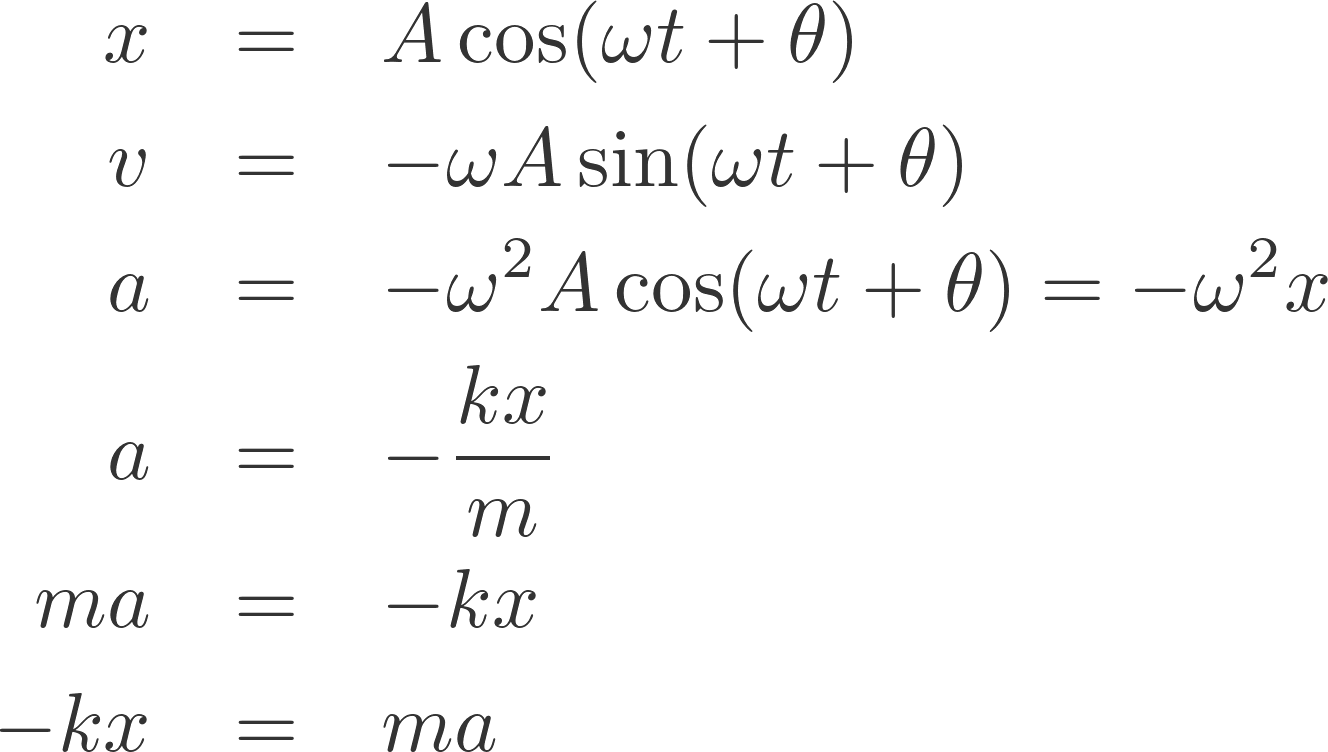
cos のカッコの中は t についている定数 ω が重要であり、バネの振動周期を決めている。

力学的エネルギー

重力のときは位置エネルギーが高さに比例したが、上図の物体は高さは変わっていない。位置エネルギーの代わりに弾性エネルギーがある。弾性エネルギーはバネが伸びれば伸びるほど、または縮めば縮むほど大きくなるようなエネルギーで

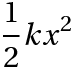
と定められる。運動エネルギーは

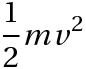
であり、力学的エネルギー E は

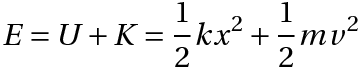
となる。E が保存すること、つまり時間で微分しても 0 になることを示す。

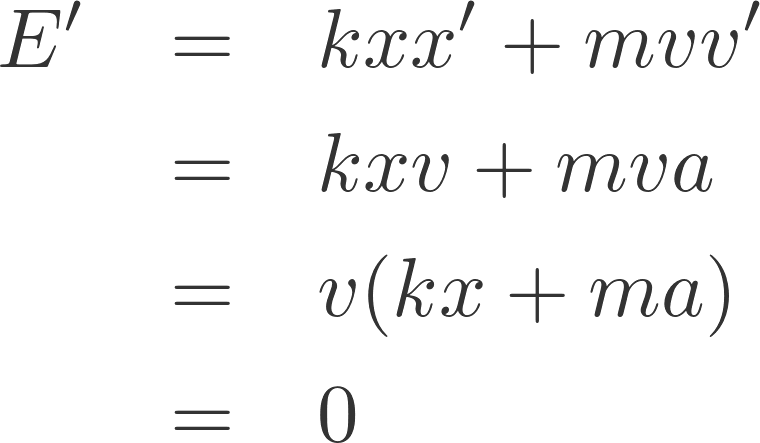
TeXコード

単振動１

x &=& A \cos \omega t \\
v &=& -\omega A \sin \omega t \\
a &=& -\omega^2 A \cos \omega t = -\omega^2 x \\
a &=& -\dfrac{kx}{m} \\
ma &=& -kx \\
-kx &=& ma

単振動２

x &=& A \cos (\omega t + \theta) \\
v &=& -\omega A \sin (\omega t + \theta) \\
a &=& -\omega^2 A \cos (\omega t + \theta) = -\omega^2 x \\
a &=& -\dfrac{kx}{m} \\
ma &=& -kx \\
-kx &=& ma

力学的エネルギー

E=U+K=\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2

保存則

E '&=&kxx '+mvv '\\
&=&kxv+mva\\
&=&v(kx+ma)\\
&=&0