三角関数の公式をTeX(LaTeX)で書くとこうなる
三角関数の公式を LaTeX で書いたものをまとめました。
加法定理
\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta
\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta
\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta
\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta
\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}
\tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}
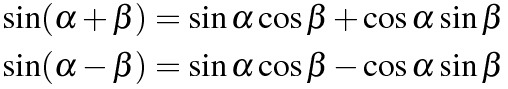
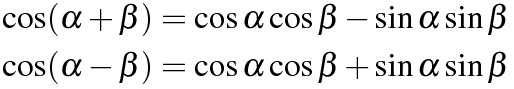
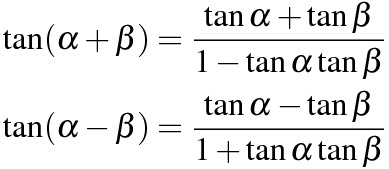
倍角公式
\sin2\alpha=2\sin\alpha\cos\beta
\begin{eqnarray*}
\cos2\alpha&=&\cos^{2}\alpha-\sin^{2}\alpha\\
&=&2\cos^{2}\alpha-1\\
&=&1-2\sin^{2}\alpha
\end{eqnarray*}
\tan2\alpha=\frac{2\tan\alpha}{1-\tan^{2}\alpha}
三倍角公式
\sin3\alpha=-4\sin^{3}\alpha+3\sin\alpha
\cos3\alpha=4\cos^{3}\alpha-3\cos\alpha
半角公式
\sin^{2}\frac{\alpha}{2}=\frac{1-\cos\alpha}{2}
\cos^{2}\frac{\alpha}{2}=\frac{1+\cos\alpha}{2}
\tan^{2}\frac{\alpha}{2}=\frac{1-\cos\alpha}{1+\cos\alpha}
積和公式
\sin\alpha\cos\beta=\frac{\sin(\alpha+\beta)+\sin(\alpha-\beta)}{2}
\cos\alpha\cos\beta=\frac{\cos(\alpha+\beta)+\cos(\alpha-\beta)}{2}
\sin\alpha\sin\beta=\frac{\cos(\alpha+\beta)-\cos(\alpha-\beta)}{2}
和積公式
\sin{A}+\sin{B}=2 \sin\frac{A+B}{2}\cos\frac{A-B}{2}
\sin{A}-\sin{B}=2 \cos\frac{A+B}{2}\sin\frac{A-B}{2}
\cos{A}+\cos{B}=2 \cos\frac{A+B}{2}\cos\frac{A-B}{2}
\cos{A}-\cos{B}=-2 \sin\frac{A+B}{2}\sin\frac{A-B}{2}
関数

-
 LaTeX記法 三角関数、逆三角関数、双曲線関数
LaTeX記法 三角関数、逆三角関数、双曲線関数0
3304
-
 LaTeX記法 べき乗と指数関数
LaTeX記法 べき乗と指数関数0
47849
-
 LaTeXコマンド 対数関数(log)と自然対数(ln)
LaTeXコマンド 対数関数(log)と自然対数(ln)0
7610
-

-
 三角関数の公式をTeX(LaTeX)で書くとこうなる
三角関数の公式をTeX(LaTeX)で書くとこうなる0
6126




