つるかめ算の面積図による解き方とポイント

例題

つるとかめが合わせて7匹いた。つるとかめの足は全部で18本だった。つるとかめはそれぞれ何匹いるか？

解答

つるの足は2本、かめの足は4本です。つるの数をよこ、つるの1匹あたりの足の数（2本）をたてとする長方形と、かめの数をよこ、かめの1匹あたりの足の数（4本）をたてとする長方形をつなげると、下図のようになります。

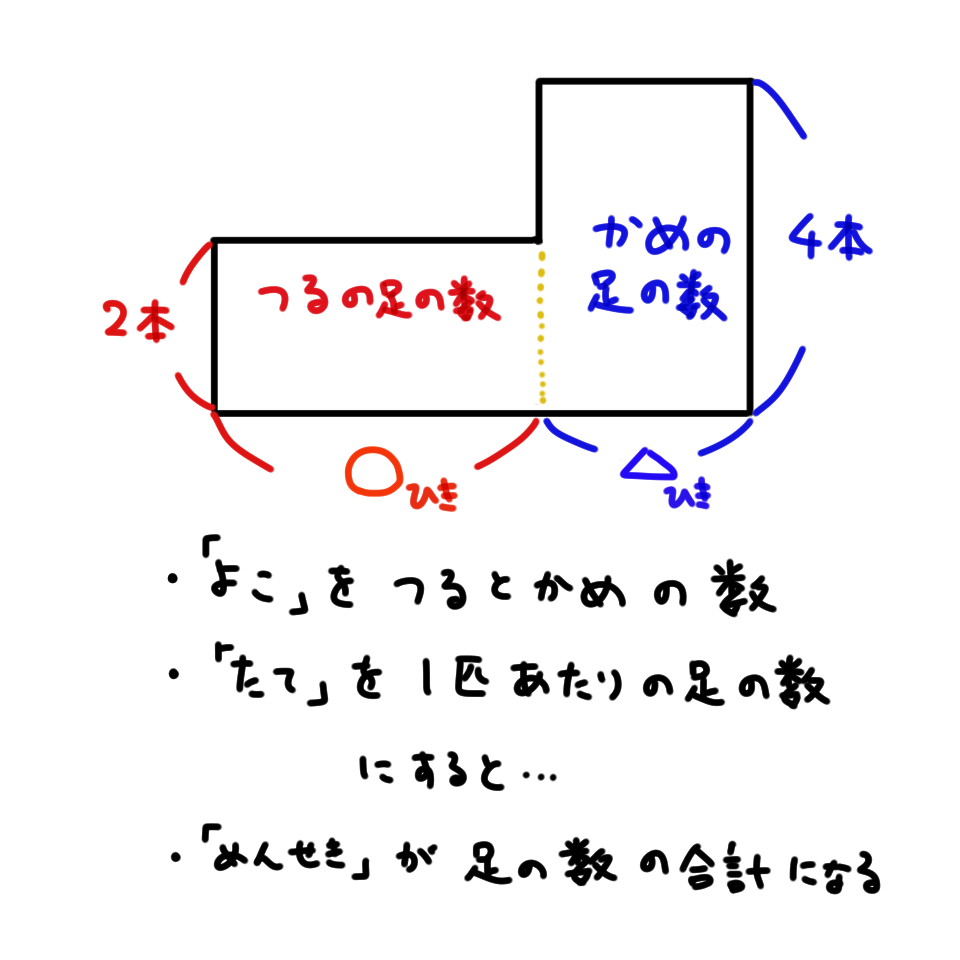
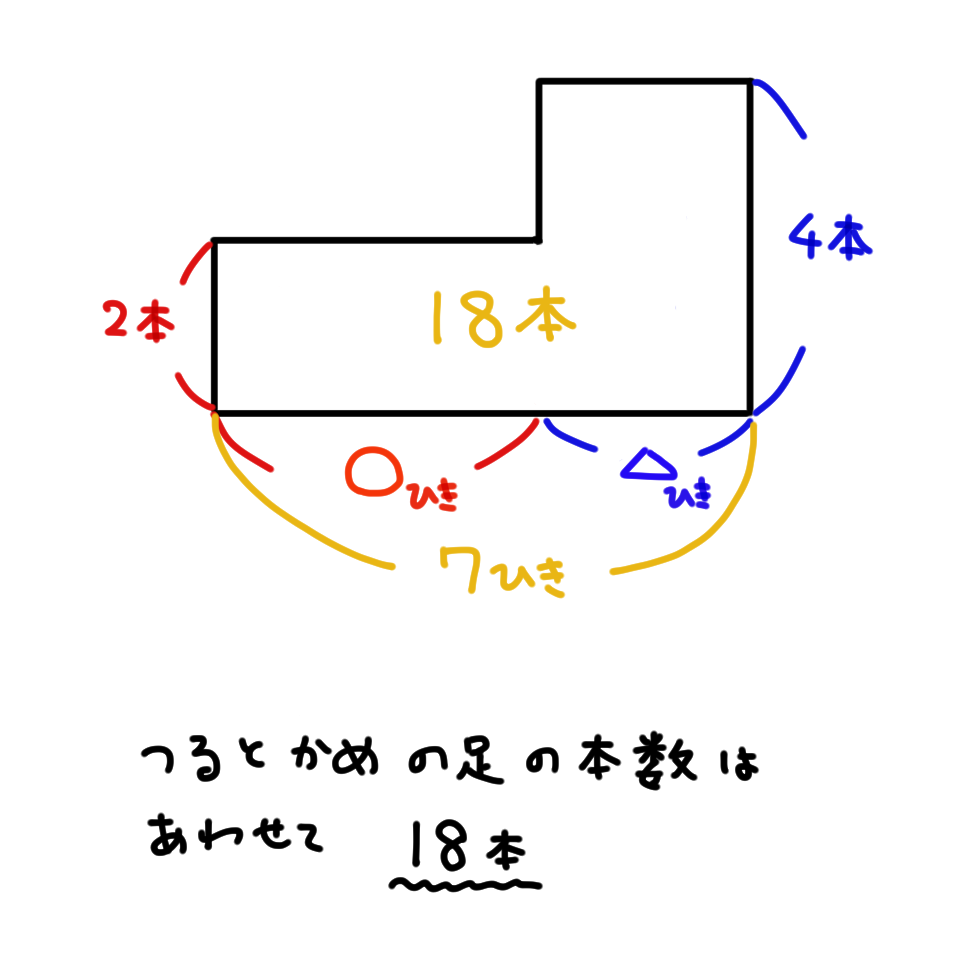
まず「大きな長方形」の面積を求めます。

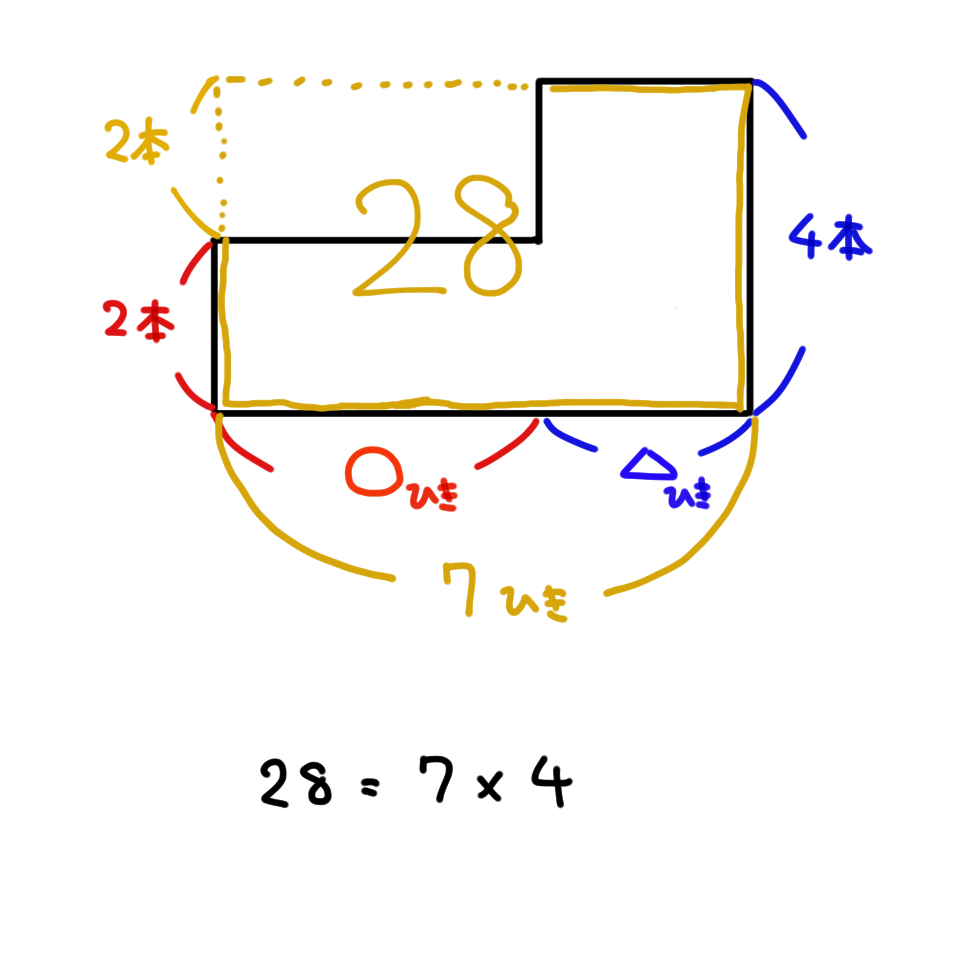
次に「空白の長方形」の面積を求めます。緑色の長方形に注目してください。

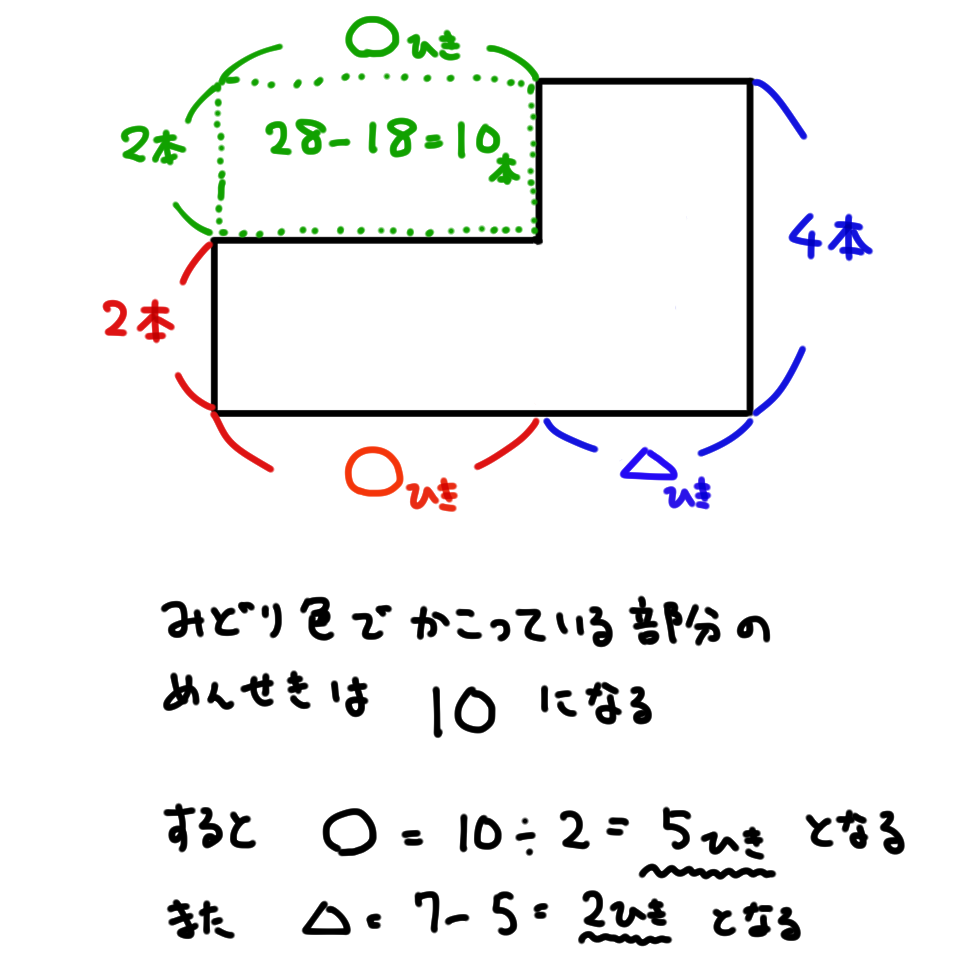
黄色で書いた「大きな長方形」から元の形を引くと、緑色の「空白の長方形」の面積が出てきます。

後はこの「空白の長方形」の面積をかめの足とつるの足の差（2=4-2）で割ると、つるの数が求まります。

以上から

つる5匹
かめ2匹

となります。

問題

太郎くんはみかんとりんごを合わせて18個買い、700円払った。みかんは1個あたり30円、りんごは1個あたり50円である。太郎くんはみかんとりんごをそれぞれ何個ずつ買ったか？

解答

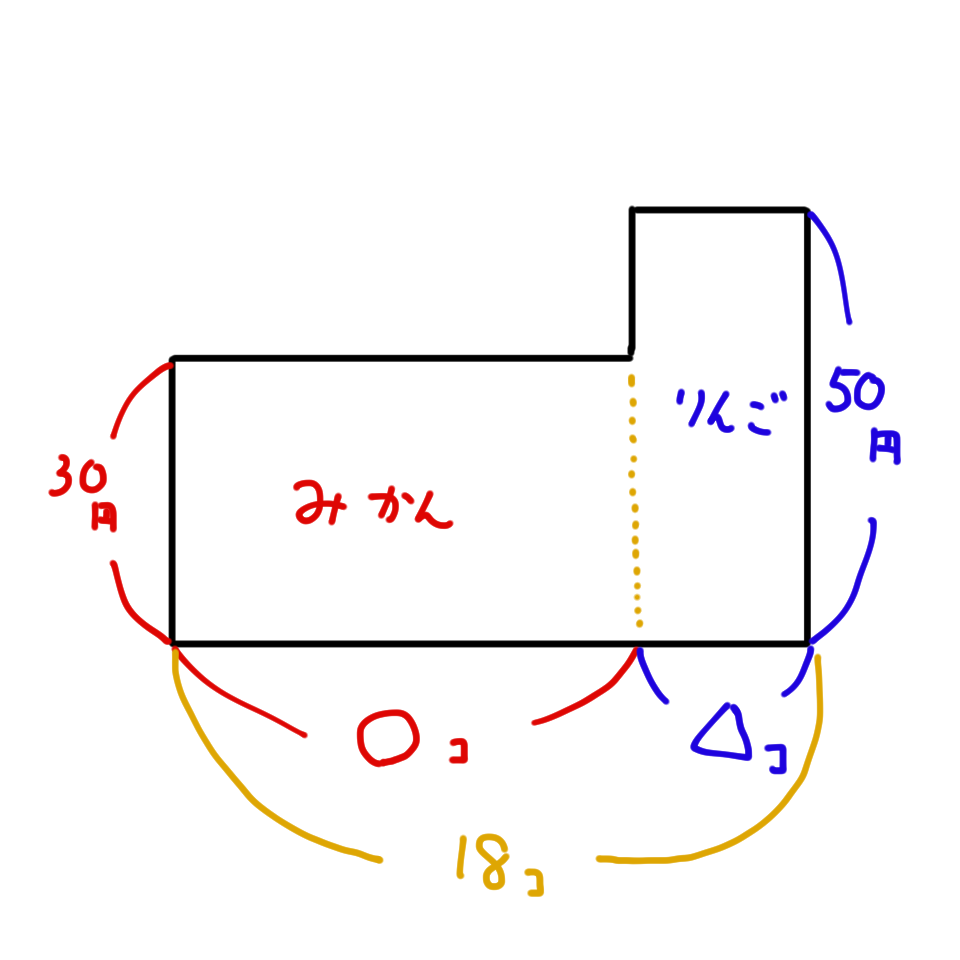
みかんが左の長方形、りんごが右の長方形です。長方形のよこは個数、たては一個あたりの値段、面積は全体の値段になります。

一方、二つの長方形を合わせた面積は700円となります。

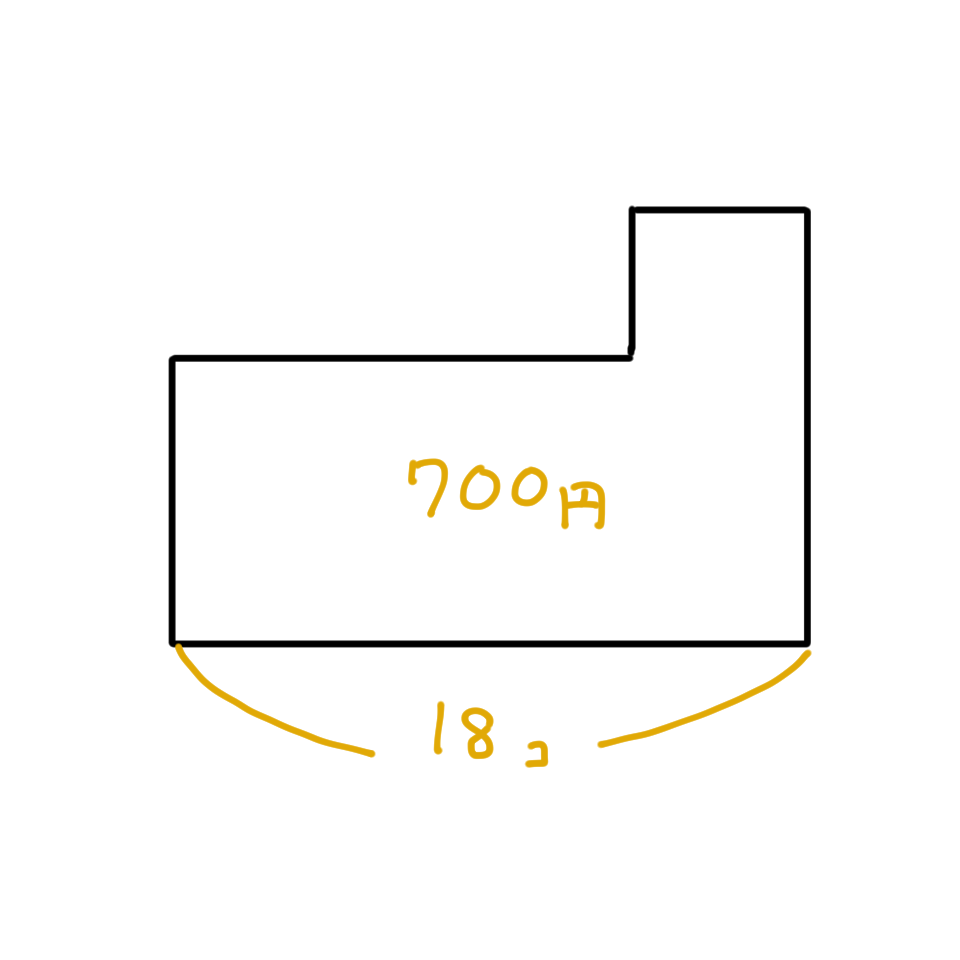
ここまできたら、先ほどと同じように「大きな長方形」の面積を求めます。底辺が18個、高さがりんごの一個あたりの値段である50円の長方形です。

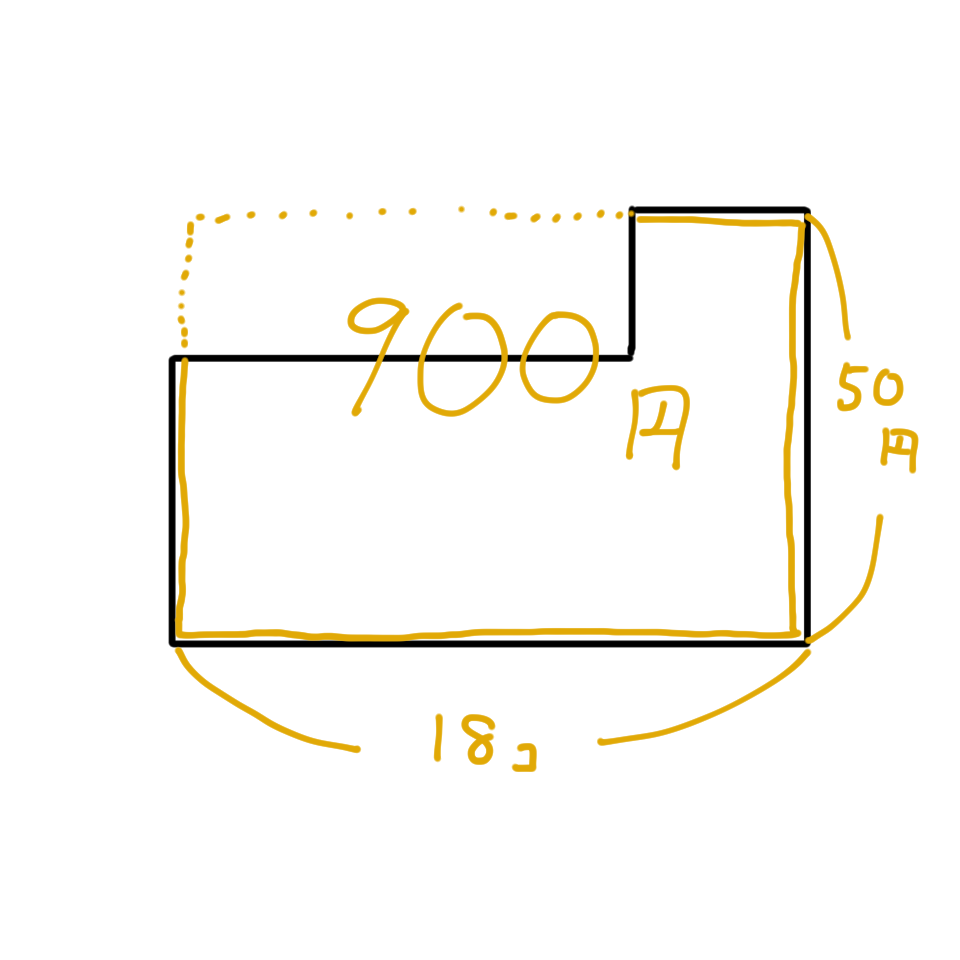
あとはこの「大きな長方形」から元の図形を引いた「空白の長方形」の面積を求めます。

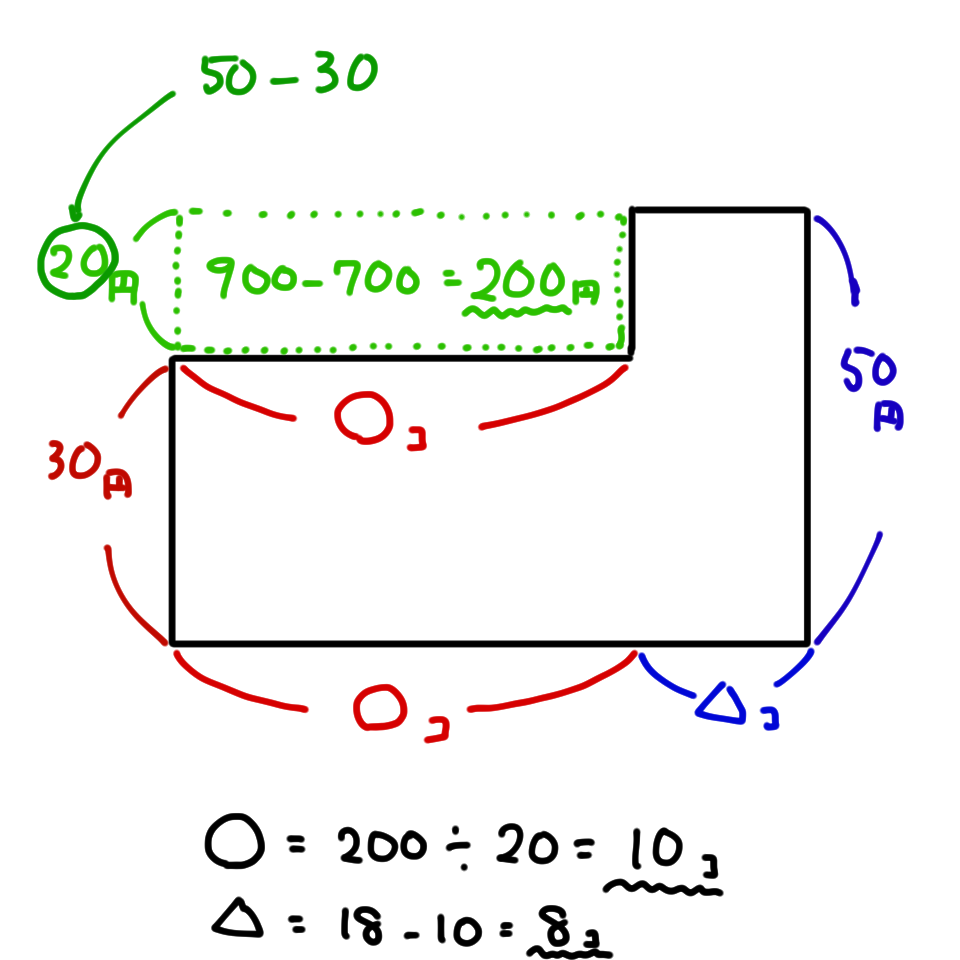
この「空白の長方形」は900-700=200円となり、りんごとみかんの差額である20円で割ると、◯に相当する底辺の長さが10個と求まります。

最後の仕上げにりんごの数を全体の個数からみかんの数10個で引いて18-10=8個と求めます。

みかん10個
りんご8個