相関係数の意味と公式:具体例から計算方法と求め方を理解しよう(標準偏差と共分散の復習つき)
相関係数とは、二つのデータが相関しているかを表すものです。100 人が数学と物理の試験を受けたとき、数学の点が高い人ほど物理の点も高いといった傾向があったとします。この傾向の強さを相関係数で具体的に表します。
相関係数の意味
二つ(またはそれ以上)のデータの相関性を示すもの。
相関係数の計算方法と求め方
A〜D の生徒が数学と物理の試験を受けて、それぞれ次の点数になったとします。
| 生徒 | 数学 | 物理 |
|---|---|---|
| A | 100 | 90 |
| B | 20 | 10 |
| C | 70 | 80 |
| D | 50 | 40 |
見てわかるように、数学と物理の点がかなり相関しています(正確に言うなら「正に相関している」)。
実際に数学と物理の相関係数を計算してみましょう。次の手順で求めます。
- 数学の標準偏差を求める(A とする)
- 物理の標準偏差を求める(B とする)
- A と B をかけ算する(C とする)
- 数学と物理の共分散を求める(D とする)
- D ÷ C が相関係数になる
数学の標準偏差
標準偏差とは「データのばらつき」です。まずは平均を求めます。
(100 + 20 + 70 + 50) ÷ 4 = 60
次に各データと平均の差を求める。例えば A は 100 で平均は 60 なので、差は 40 になります。
| 生徒 | 数学 | 平均との差 |
|---|---|---|
| A | 100 | 40 |
| B | 20 | 40 |
| C | 70 | 10 |
| D | 50 | 10 |
そして差の二乗を計算します。
| 生徒 | 数学 | 差 | 差の二乗 |
|---|---|---|---|
| A | 100 | 40 | 1600 |
| B | 20 | 40 | 1600 |
| C | 70 | 10 | 100 |
| D | 50 | 10 | 100 |
「差の二乗」の平均を求めます。
1600 + 1600 + 100 + 100 = 3400
3400 ÷ 4 = 850
これの平方根(ルート 850)を計算します。
29.154
ざっくり 29.2 とします。これが数学の標準偏差です。
☆標準偏差の求め方をおさらい
- 平均を求める
- 各生徒において点数と平均の差を求める
- 各生徒において「平均の差」の二乗を求める
- 「二乗」の平均を求める
物理の標準偏差
まずは平均を求めます。
(90 + 10 + 80 + 40) ÷ 4 = 55
平均差を求める。例えば A は 90 で平均は 55 なので、差は 35 になります。
| 生徒 | 物理 | 平均との差 |
|---|---|---|
| A | 90 | 35 |
| B | 10 | 45 |
| C | 80 | 25 |
| D | 40 | 15 |
そして差の二乗を計算します。
| 生徒 | 物理 | 差 | 差の二乗 |
|---|---|---|---|
| A | 90 | 35 | 1225 |
| B | 10 | 45 | 2025 |
| C | 80 | 25 | 625 |
| D | 40 | 15 | 225 |
「差の二乗」の平均を求める。
1225 + 2025 + 625 + 225 = 4100
4100 ÷ 4 = 1025
これの平方根(ルート 1025)を計算します。
32.015
ざっくり 32.0 とします。これが物理の標準偏差です。
標準偏差の積
数学の標準偏差 29.2
物理の標準偏差 32.0
29.2 × 32.0 = 934.4
数学と物理の共分散
共分散は計算がとても大変です。共分散の計算はエクセルなどのソフトを使うことを勧めます。
まずは数学と物理の各データ差をもう一度見てください。
| 生徒 | 数学 | 平均との差 |
|---|---|---|
| A | 100 | 40 |
| B | 20 | 40 |
| C | 70 | 10 |
| D | 50 | 10 |
| 生徒 | 物理 | 平均との差 |
|---|---|---|
| A | 90 | 35 |
| B | 10 | 45 |
| C | 80 | 25 |
| D | 40 | 15 |
数学と物理の差を生徒ごとにかけ算します。
| 生徒 | 数学差 | 物理差 | 差の積 |
|---|---|---|---|
| A | 40 | 35 | 1400 |
| B | 40 | 45 | 1800 |
| C | 10 | 25 | 250 |
| D | 10 | 15 | 150 |
この「差の積」の平均を求めます。
1400 + 1800 + 250 + 150 = 3600
3600 ÷ 4 = 900
相関係数を計算する
相関係数は
共分散 ÷ 標準偏差の積
で求まるため、例における相関係数は
900 ÷ 934.4 ≒ 0.96
となります。0.96 が相関係数です。
相関係数の公式
$2$ つの $n$ 個のデータ
\[ x=(x_{1},\ x_{2},\ \cdots,\ x_{n})\\ y=(y_{1},\ y_{2},\ \cdots,\ y_{n}) \]
を考える。
\[ \overline{x}=\frac{1}{n}\sum_{i=1}^{n}x_{i} \]
\[ \overline{y}=\frac{1}{n}\sum_{i=1}^{n}y_{i} \]
とする(すなわち $\overline{x}$ はデータ $x$ の平均値、 $\overline{y}$ はデータ $y$ の平均値)。このとき分散(VAR)と共分散(COV)と相関係数(COR)を次のように定義する。
\[ (\mathrm{VAR})\ \ \sigma_{x}^{2}=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\overline{x})^{2} \]
\[ (\mathrm{VAR})\ \ \sigma_{y}^{2}=\frac{1}{n}\sum_{i=1}^{n}(y_{i}-\overline{y})^{2} \]
\[ (\mathrm{COV})\ \ \sigma_{xy}=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y}) \]
\[ (\mathrm{COR})\ \ \rho_{xy}=\frac{\sigma_{xy}}{\sigma_{x}\sigma_{y}} \]
共分散の求め方(エクセルの例)
生徒 $1$ から $10$ までの英数理の点数の共分散をエクセルで求めてみよう。以下、エクセルのスクリーンショットとコマンドは「Office365」である。
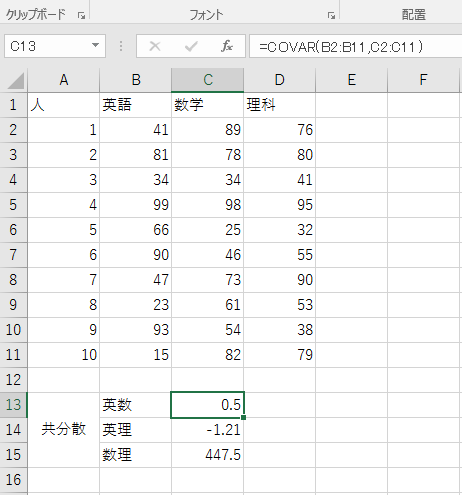
英語と数学の共分散を調べる。英語はB列、数学はC列。共分散のコマンドは「COVAR」で、変数は「◯:◯,◯:◯」とする。カンマの前は英語データ、カンマの後は数学データであり、コロンで列の最初と最後を区切る。つまり
=COVAR(B2:B11,C2:C11)
で英語と数学の共分散が求まる。同様に英語と理科、数学と理科の共分散は次の式で求まる。
英語と数学=COVAR(B2:B11,C2:C11)
英語と理科=COVAR(B2:B11,D2:D11)
数学と理科=COVAR(C2:C11,D2:D11)
エクセルの計算によって英語と数学、英語と理科の共分散は $0$ に近く、数学と理科の共分散はかなり大きいことがわかった。
相関係数の求め方(エクセルの例)
上の英数理の点数データを使って、今度は相関係数をエクセルで求めてみよう。
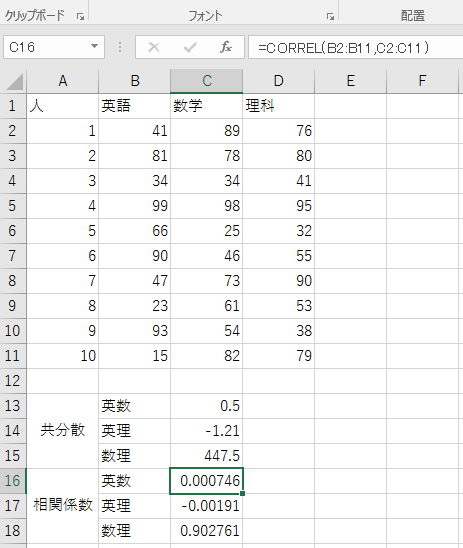
相関係数のコマンドは「CORREL」で、変数は共分散と同様に「◯:◯,◯:◯」とする。カンマの前は英語データ、カンマの後は数学データであり、コロンで列の最初と最後を区切る。つまり
=CORREL(B2:B11,C2:C11)
で英語と数学の共分散が求まる。同様に英語と理科、数学と理科の共分散は次の式で求まる。
英語と数学=CORREL(B2:B11,C2:C11)
英語と理科=CORREL(B2:B11,D2:D11)
数学と理科=CORREL(C2:C11,D2:D11)
エクセルの計算によって英語と数学、英語と理科の共分散は $0$ に近く、数学と理科の共分散は $1$ に近いことがわかった。
共分散と相関係数の意味
共分散が正または負に大きい ↔ 二つのデータに関係がある
共分散が $0$ に近い ↔ 二つのデータはあまり関係がない
相関係数が $1$ に近い ↔ 二つのデータに関係がある
相関係数が $0$ に近い ↔ 二つのデータはあまり関係がない
共分散と相関係数の意味は上の通りである。どちらも $0$ に近ければ近いほどデータ間の関係が薄くなるということ。共分散と相関係数はどちらもデータ間の関係性を示す。
上のエクセルのデータ、英数理の点数を見ればわかるように、明らかに英語と数学に関係がない。英語で高得点だから数学でも高得点かというとそうでもない。逆に英語で赤点をとっている人が数学でいい点をとっている。
一方、数学と理科は明らかに関係している。数学で点をとっている人は理科でも点をとっており、理科で点をとっている人は数学でも点をとっている。
この「見た目の関係性」がきちんと共分散と相関係数という数学的な値に反映されていることに注目しよう。
共分散の公式の変形
最初にあげた共分散と相関係数の公式は実用上使いにくい。そのため次のように変形する。
\begin{split} \sigma_{xy}&=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})\\ &=\frac{1}{n}\sum_{i=1}^{n}(x_{i}y_{i}-\overline{x}y_{i}-\overline{y}x_{i}+\overline{x}\overline{y})\\ &=\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i}-\frac{1}{n}\sum_{i=1}^{n}\overline{x}y_{i}\\ &\quad-\frac{1}{n}\sum_{i=1}^{n}\overline{y}x_{i}+\frac{1}{n}\sum_{i=1}^{n}\overline{x}\overline{y} \end{split}
ここで $\overline{x},\ \overline{y}$ は定数である(それぞれデータの平均値であることを思い出そう)から、上の式の第 $2$ 項、第 $3$ 項、第 $4$ 項は
\begin{equation*} \begin{split} \frac{1}{n}\sum_{i=1}^{n}\overline{x}y_{i}&=\overline{x}\cdot\frac{1}{n}\sum_{i=1}^{n}y_{i}\\ &=\overline{x}\overline{y} \end{split} \end{equation*} \begin{equation*} \begin{split} \frac{1}{n}\sum_{i=1}^{n}\overline{y}x_{i}&=\overline{y}\cdot\frac{1}{n}\sum_{i=1}^{n}x_{i}\\ &=\overline{y}\overline{x} \end{split} \end{equation*} \begin{equation*} \begin{split} \frac{1}{n}\sum_{i=1}^{n}\overline{x}\overline{y}&=\overline{x}\overline{y}\cdot\frac{1}{n}\sum_{i=1}^{n}1\\ &=\overline{x}\overline{y}\cdot\frac{1}{n}\cdot{n}\\ &=\overline{x}\overline{y} \end{split} \end{equation*}
となる。したがって
\begin{equation*} \begin{split} \sigma_{xy}&=\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i}-\frac{1}{n}\sum_{i=1}^{n}\overline{x}y_{i}\\ &\quad-\frac{1}{n}\sum_{i=1}^{n}\overline{y}x_{i}+\frac{1}{n}\sum_{i=1}^{n}\overline{x}\overline{y}\\ &=\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i}-\overline{x}\overline{y}-\overline{x}\overline{y}+\overline{x}\overline{y}\\ &=\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i}-\overline{x}\overline{y} \end{split} \end{equation*}
となる。
\[ \sigma_{xy}=\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i}-\overline{x}\overline{y} \]
この式は非常に重要であり、実用的である。
もう少し詳しい相関(正の相関と負の相関)
相関は正の相関と負の相関がある。例えば英語と数学の点数の相関についてもう一度考える。
例えば英語の点数が高くなるほど、数学の点数が高くなるとする。このとき英語と数学の点数は正の相関にあるという。
逆に英語の点数が高くなるほど、数学の点数が低くなるとする。このとき英語と数学の点数は負の相関にあるという。
正の相関
英語↑ ⇒ 数学↑
英語↓ ⇒ 数学↓
負の相関
英語↑ ⇒ 数学↓
英語↓ ⇒ 数学↑
データ間の関係が正の相関にあるか、負の相関にあるかは相関係数で判断できる。
・相関係数が $1$ に近いほど、正の相関が強い。
・相関係数が $-1$ に近いほど、負の相関が強い。
ここで相関係数についてもう一つの数学的な性質が重要になる。
\[ -1\leqq\rho_{xy}\leqq{1} \]
実は相関係数は $-1$ 未満にならず、また $1$ より大きくもならない。現実問題としてデータとデータが完全に相関するということはないが、数学と物理の点数の相関係数はかなり $1$ に近いかもしれない…。
数学用語の英訳
分散 … variance
共分散 … covariance
相関係数 … correlation coefficient
エクセルの関数名はこれらのスペルからとっている。
統計

-

-
 確率変数の期待値と分散と標準偏差の公式と意味
確率変数の期待値と分散と標準偏差の公式と意味0
1150
-
 確率変数の変換と期待値、分散、標準偏差の変換公式
確率変数の変換と期待値、分散、標準偏差の変換公式0
2011
-

-

-

-
 統計学入門 (基礎統計学)の評価と使い方
統計学入門 (基礎統計学)の評価と使い方0
908
-

-





