等比数列とは？等比数列の意味と性質、一般項と和の公式をわかりやすく解説

等比数列とは、同じ数をかけてできる数列です。等差数列は同じ数を足していきますが、等比数列は同じ数をかけていきます。例えば

\[ 2,\ 6,\ 18,\ 54,\ \cdots \]

は初項 $2$、公比 $3$ の等比数列です。最初の数を初項といい、かけていく数を公比といいます。

\[ 6=2 \times 3 \\ 18=6 \times 3 \\ 54=18 \times 3 \\ \]

54 の次はいくつでしょうか？　この等比数列は 3 ずつかけていくため、$54 \times 3 = 162$ が次の数になります。

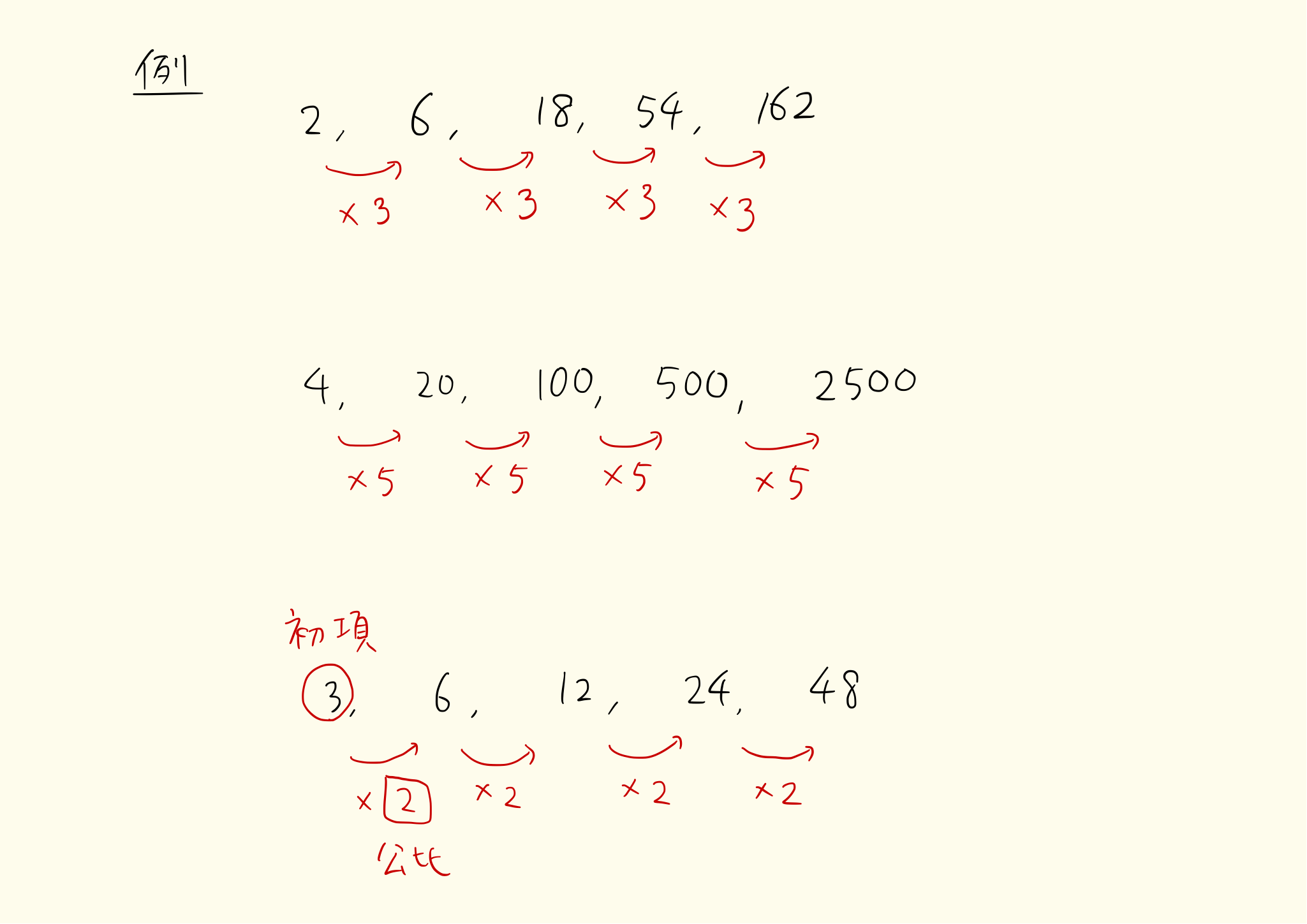
等比数列を抽象的に考える

初項が $a$ で、公比が $r$ の等比数列を考えてください。

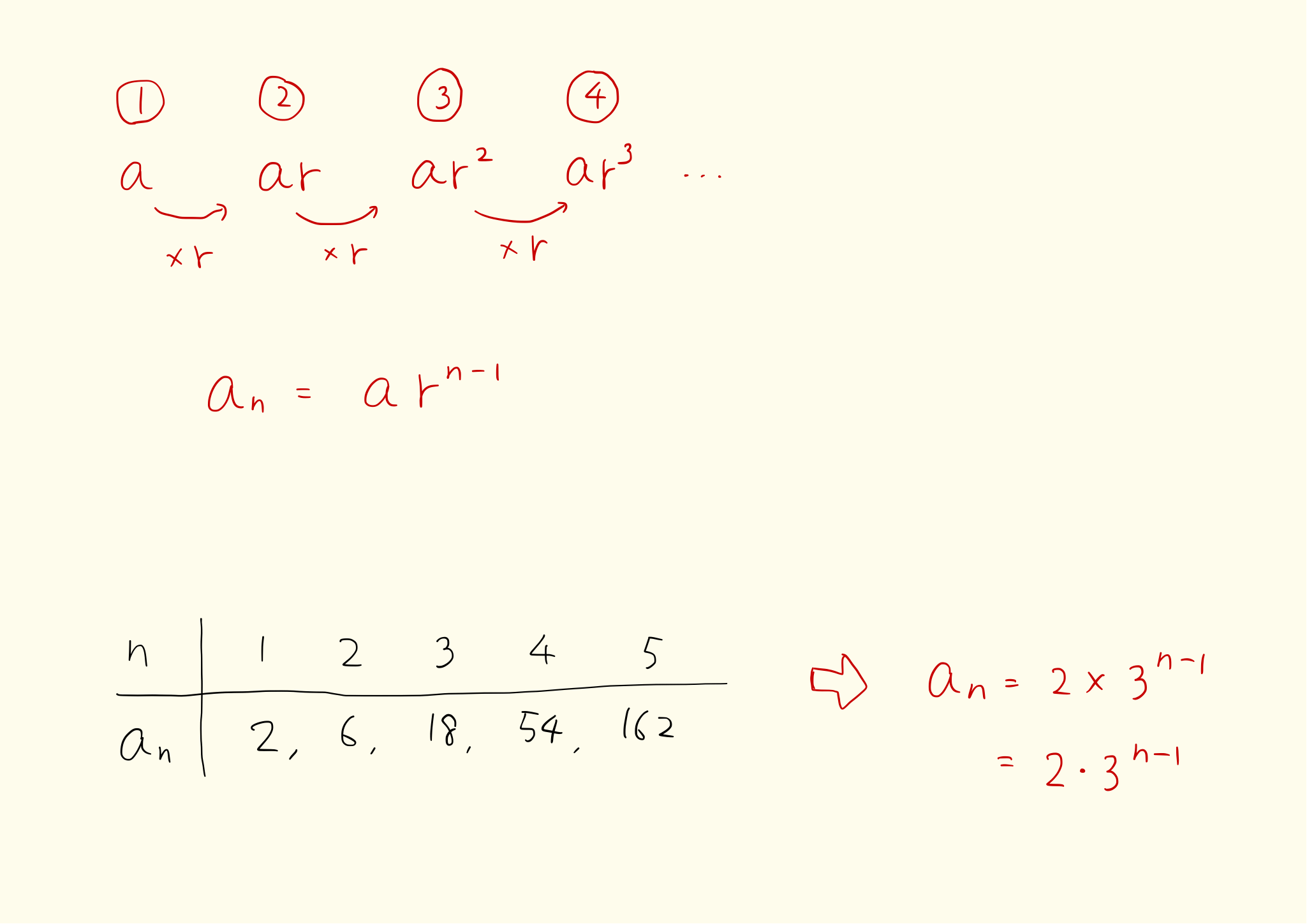
プリントにあるように $a,\ ar,\ ar^2$ と数が続きます。$r$ の右肩についている数（次数）を見てください。$3$ 番目の数は $r^2$ で、$4$ 番目の数は $r^3$ となっています。

つまり $n$ 番目の次数は $n-1$ です。この法則を理解すると、10 番目の数や 100 番目の数も計算できるようになります。実際、その計算が高校数学の等比数列で一番大切なところです。

等比数列の一般項

一般項とは、n 番目の数を n で表したものです。等比数列の一般項（n 番目の数）は初項 a に r の n-1 乗をかけた数です。

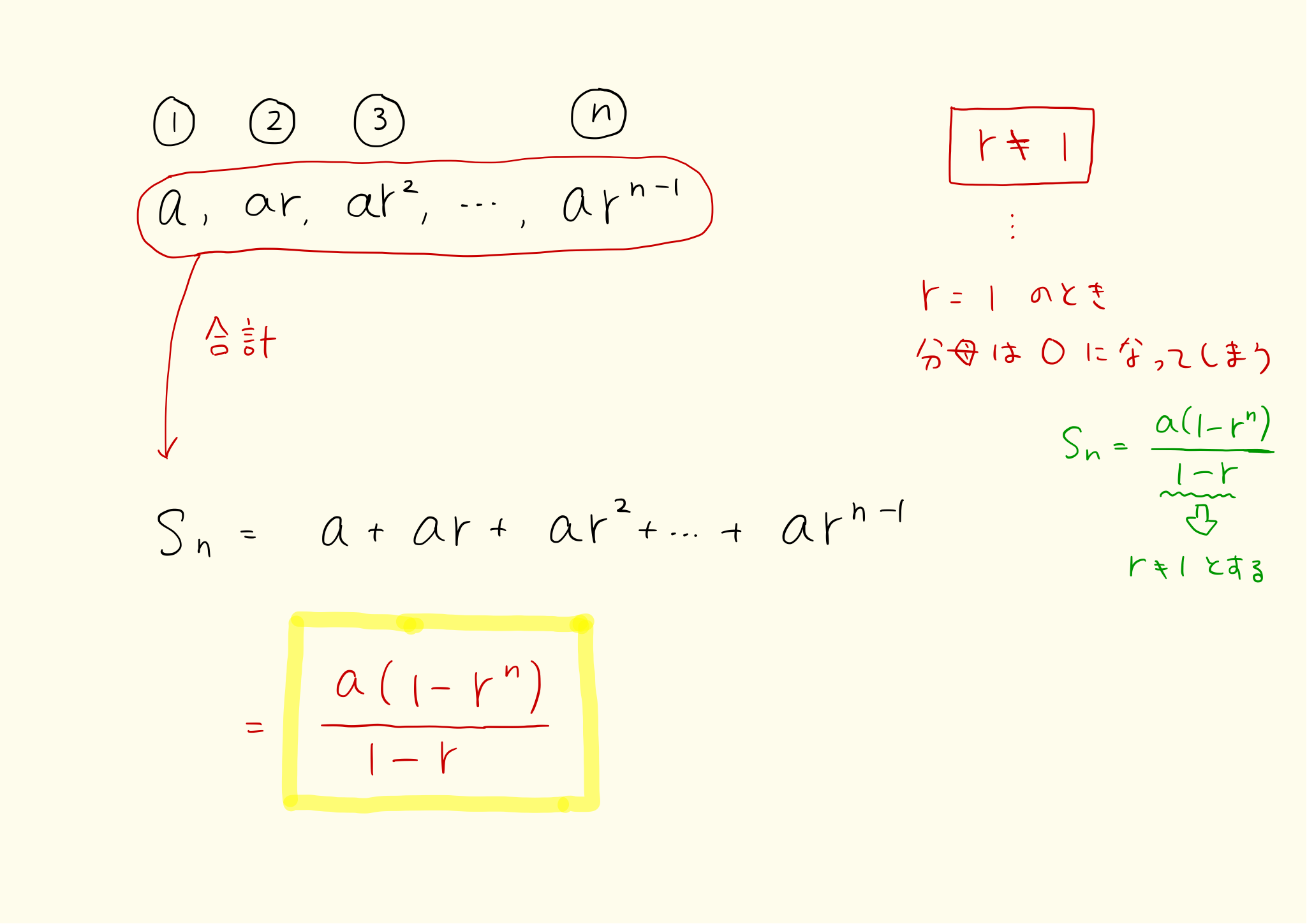
（プリントの上だけを見てください）

等比数列の一般項

\[ a_{n}= a r^{n-1} \ (r \neq 1) \]

等比数列の和の公式

等比数列の和の公式は 2 つあります。

\[ S_n=an \ (r=1) \]

\[ S_{n}=a\dfrac {1-r^{n}}{1-r} \ (r \neq 1) \]

それぞれの公式をくわしく考えよう。

等比数列の和の公式（公比が 1 のとき）

まずは公比が 1 のとき。つまり $r=1$ のとき、等比数列の和 $S_n$ は

\[ S_n=an \]

となります。ただし $a$ は等比数列の初項。初項が $1$ のときは等比数列のすべての項が $a$ になるので、その和は $a$ を $n$ 倍した値です。

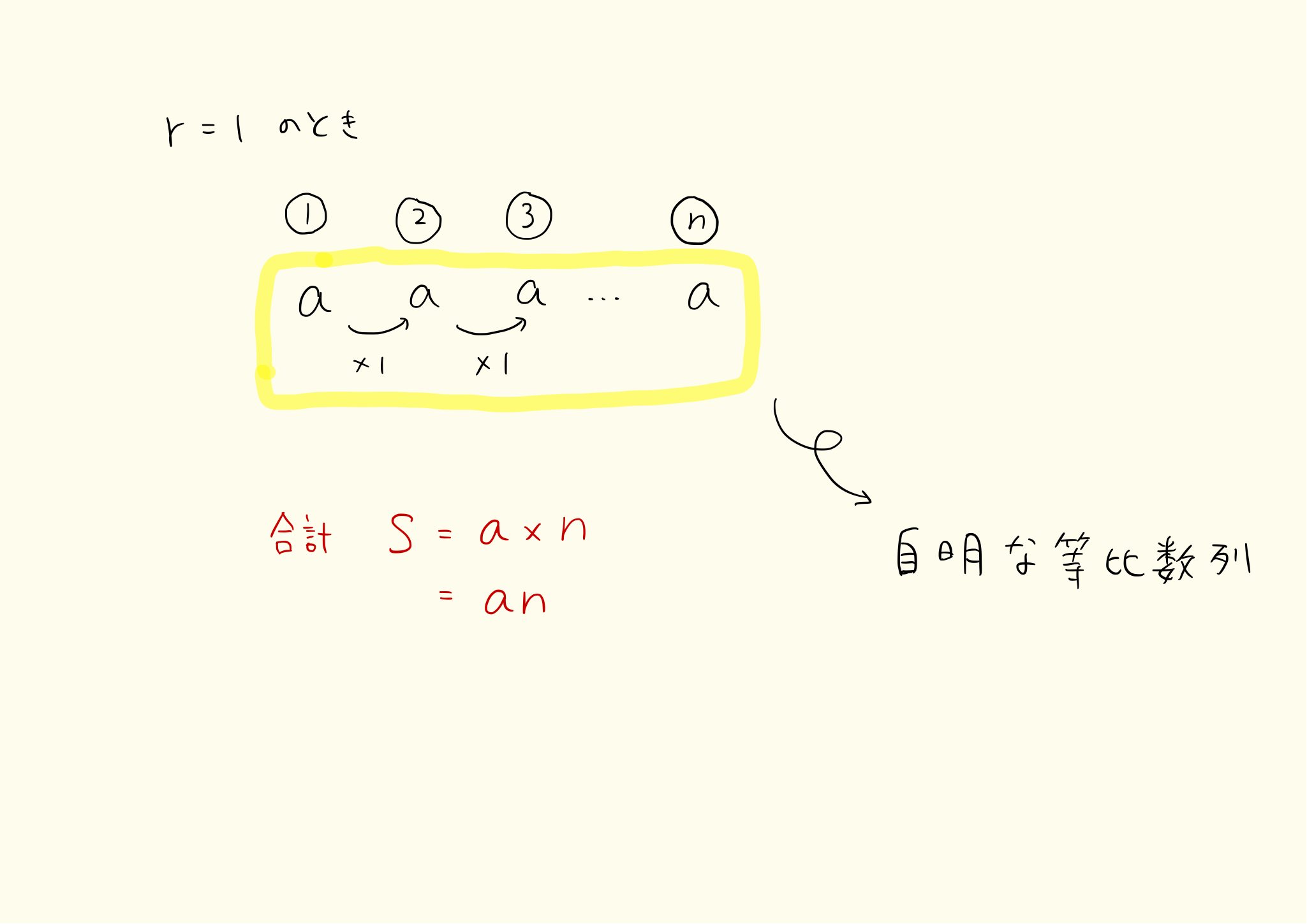
等比数列の和の公式（公比が 1 でないとき）

等比数列の公比が 1 でないとき。

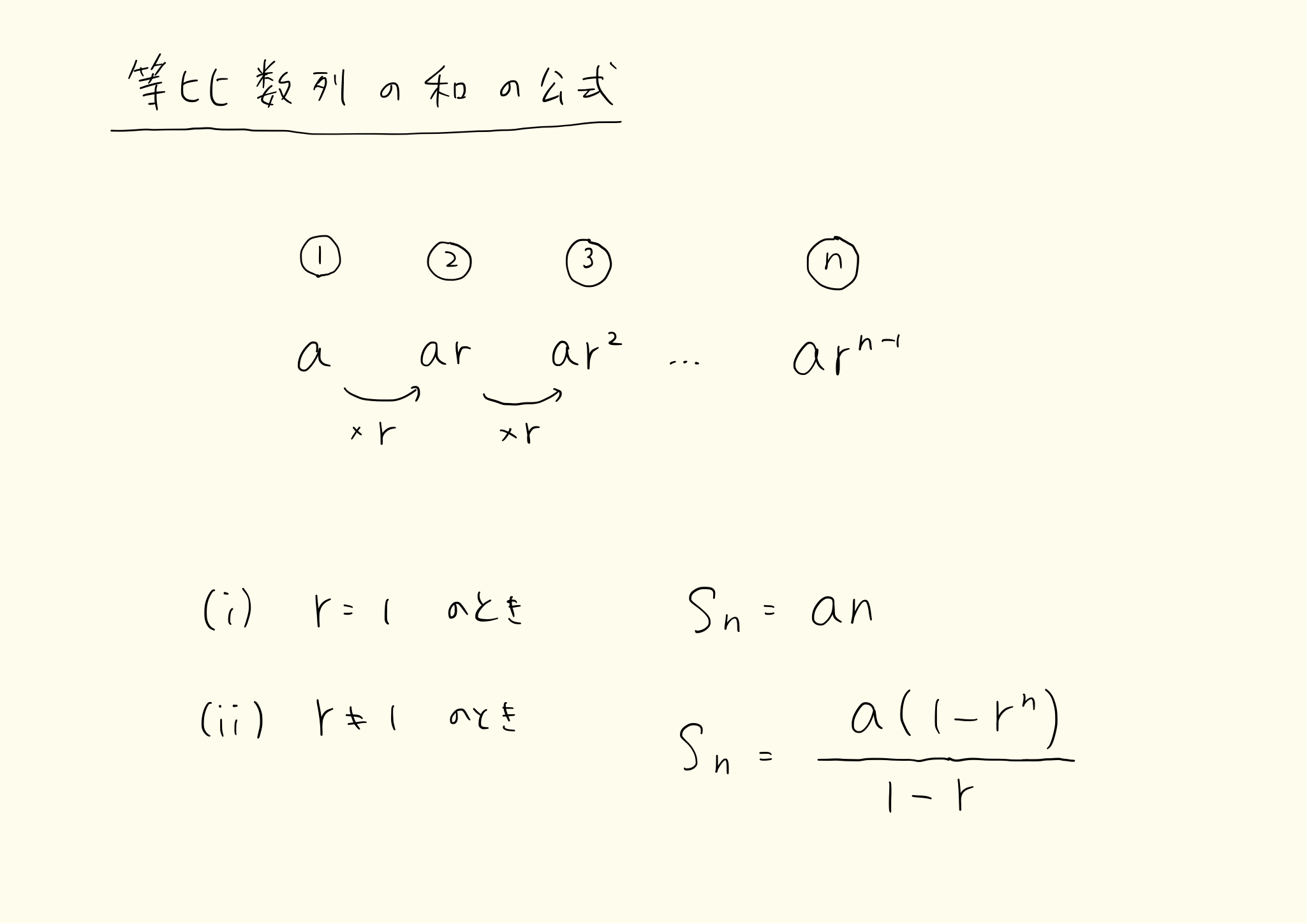
等比数列の和の公式が正しいことを確かめる

実際の数列を用いて、等比数列の和の公式

\[ S_{n}=a\dfrac {1-r^{n}}{1-r} \ (r \neq 1) \]

が正しいことを確認しましょう。はじめに出てきた

\[ 2,\ 6,\ 18,\ 54 \]

は、初項 2 で公比 3 の等比数列です。この等比数列の和は 2 + 6 + 18 + 54 = 80 です。

では、等比数列の和の公式を使って求めてみましょう。数は 4 つしかないので、n = 4 です。

\[ S_{4} = 2 \dfrac {1-3^{4}}{1-3} \\ = 2 \times \dfrac {80}{2} \\ = 2 \times 40 \\ = 80 \]

となり、等比数列の和の公式が正しいことがわかりました。

（追記中）