一次関数のグラフの書き方(プロットのやり方、切片と傾きの意味)
$y = 2x + 1$ のように $y = ax + b$ という形の関数を一次関数といいます。次の関数はすべて一次関数です。
\[ y = x + 5 \\ y = 3x + 7 \\ y = 6x - 9 \\ y = 100x + 200 \\ y = -5x + 1 \]
代入
$y = 2x + 1$ は $x = 0$ のとき $y = 1$ となり、$x = 1$ のとき $y = 3$ となります。
\[ 2 \cdot 0 + 1 = 1 \\ 2 \cdot 1 + 1 = 3 \]
一次関数 $y = 2x + 1$ の $x$ にいろいろな値を入れて $x$ と $y$ の関係を調べてみよう。
| x | y |
|---|---|
| -3 | -5 |
| -2 | -3 |
| -1 | -1 |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
座標
上の表で出てきた値を図にしてみよう。
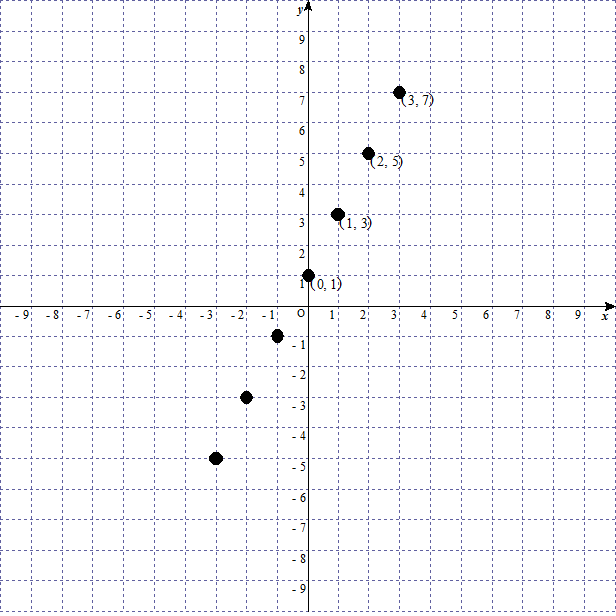
点を結び、線にする。
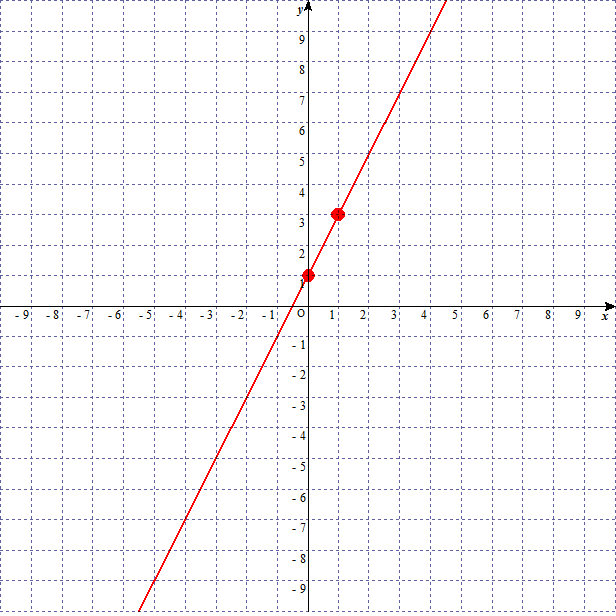
これを一次関数 $y = 2x + 1$ のグラフという。一次関数のグラフは二つのポイントがあります。
- 一次関数のグラフは直線
- 二つの点がわかればグラフがわかる
上の赤い直線も $(0,\ 1)$ と $(1,\ 3)$ の二点を結んでいる。
グラフの書き方(基本)
$y = 3x - 2$ を書いてみよう。二つの点がわかればグラフがわかるので、二つの点を適当に求める。
例えば $x$ に $1$ と $2$ を入れると
| x | y |
|---|---|
| 1 | 1 |
| 2 | 4 |
となる。つまりこのグラフは $(1,\ 1)$ と $(2,\ 4)$ の二点を通ります。
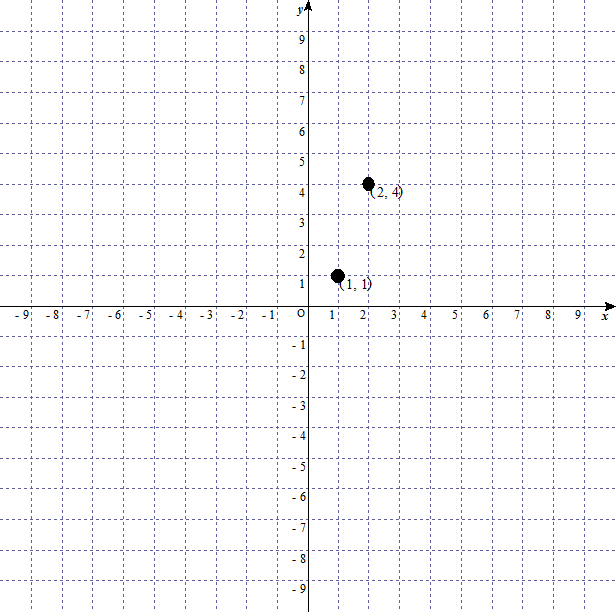
この二点を結ぶと、$y = 3x - 2$ のグラフになる。
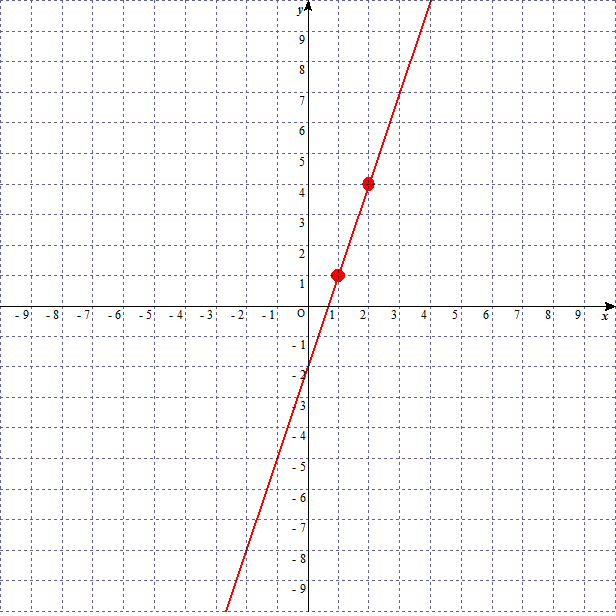
一次関数のグラフの簡単な書き方(応用)
$y=\dfrac{2}{3} x - 1$ という一次関数のグラフを書いてみよう。前問と同じように二つの点を求めますが、なるべく $y$ の値が整数になるようにします。例えば $x$ に $1$ を入れてしまうと
\[ y = \frac{2}{3} \cdot 1 - 1 = -\frac{1}{3} \]
となってしまい、座標に点をプロットしにくくなってしまう。$(1,\ -\dfrac{1}{3})$ という点を無理にとったらグラフは不正確になってしまうかも。そこで $x=3$ としてみる。この $3$ は $y=\dfrac{2}{3}x-1$ の分母の $3$ です。
\[ y = \frac{2}{3} \cdot 3 - 1 = 1 \]
きれいな数になった。つまりこのグラフは $(3,\ 1)$ を通ります。グラフを書くにはあともう一つの点が必要ですが、ここでは $x=0$ をとってみよう。
\[ y=\dfrac{2}{3}\cdot{0}-1=-1 \]
やはりきれいな数になった。整理すると
\[ \begin{array}{|c|c|} \hline x & y \\ \hline 0 & -1 \\ 3 & 1 \\ \hline \end{array} \]
となります。このグラフは $(0,\ -1)$ と $(3,\ 1)$ の二点を通る。
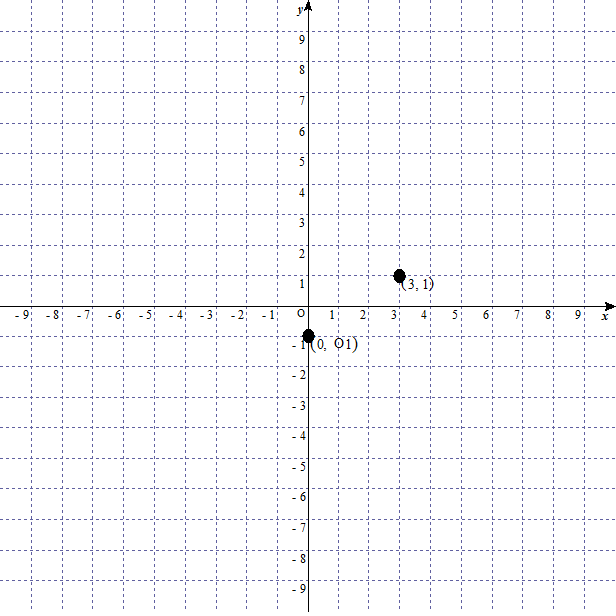
二点を結ぶと
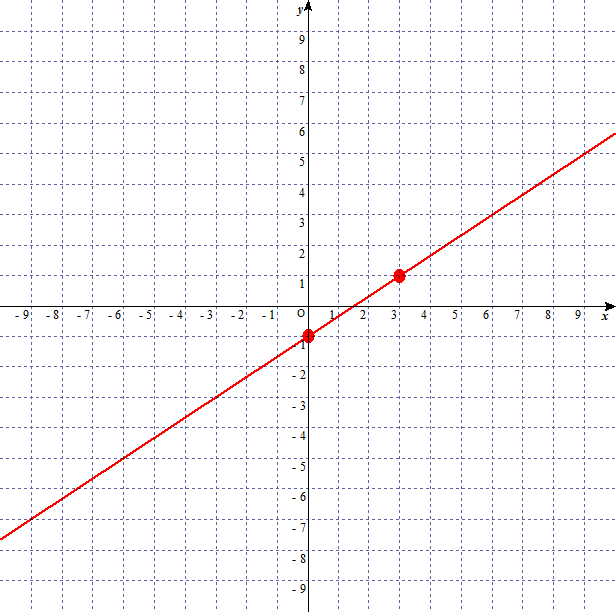
グラフが完成する。
切片
直線のグラフと $y$ 軸の交点の座標を切片といいます。例えば

の切片は、グラフと $y$ 軸が $y=1$ で交わっているから $1$ です。グラフの切片は $y=ax+b$ の $b$ に等しい。
$y=3x+5$ の切片は $5$
$y=-2x+7$ の切片は $7$
$y=x-4$ の切片は $-4$
…
本当に合っているか確かめよう。$y=3x+5$ と $y=-2x+7$ と $y=x-4$ のグラフは
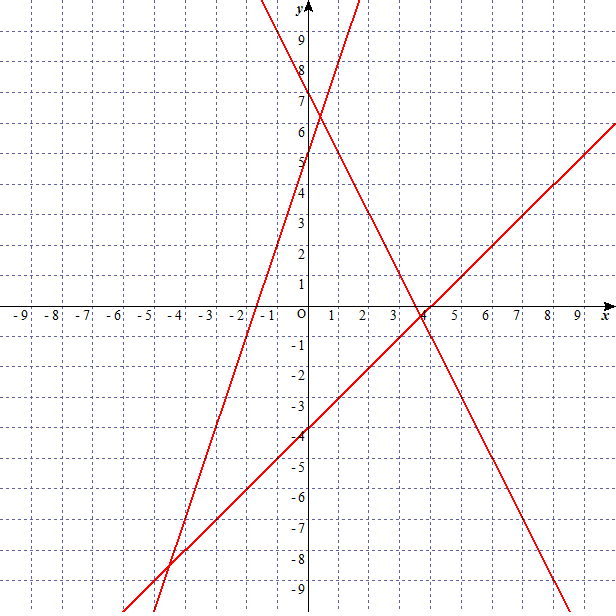
となるため、切片が合っていることがわかる。
傾き
次の三つのグラフを考える。
$y=x+1$
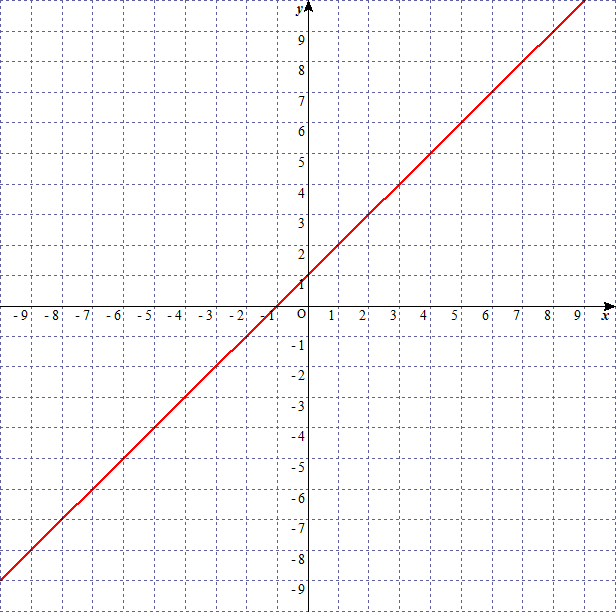
$y=2x+1$
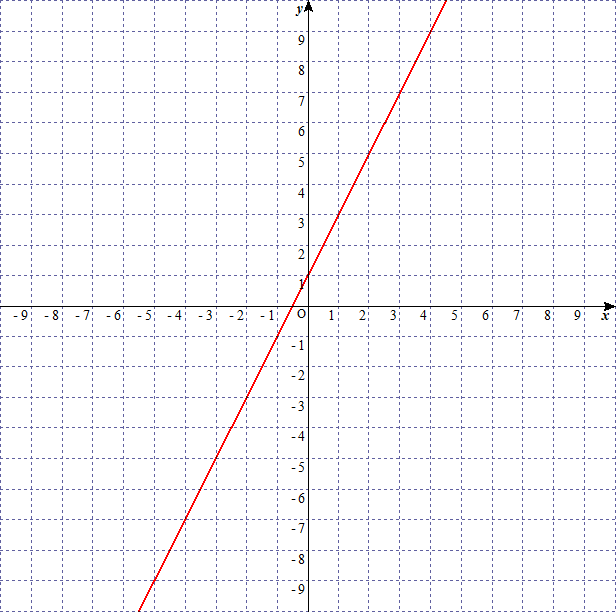
$y=3x+1$
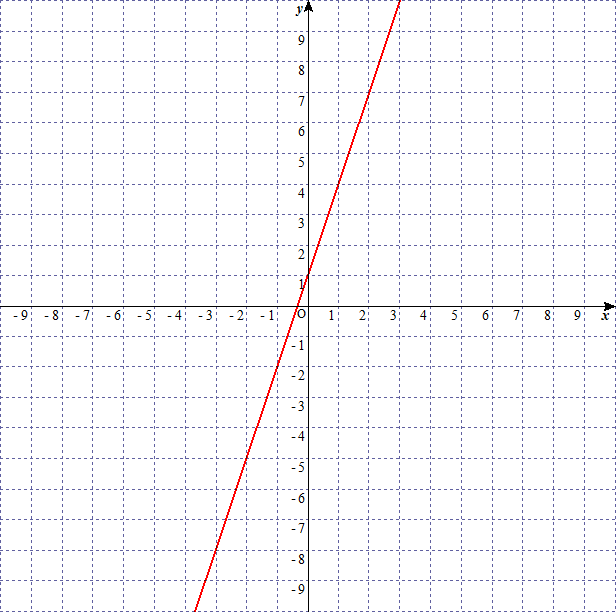
$y=ax+b$ の $a$ が大きくなればなるほど、グラフの傾きが急になっていることがわかります。このことから $y=ax+b$ の $a$ を傾きという。
例えば
$y=3x+5$ の傾きは $3$
$y=-2x+7$ の傾きは $-2$
$y=x-4$ の傾きは $1$
…
です。
中1数学

-
 中学数学 累乗の基本と計算問題(べき乗の補足説明つき)
中学数学 累乗の基本と計算問題(べき乗の補足説明つき)0
2366
-
 中学一年生 一次方程式の計算問題
中学一年生 一次方程式の計算問題0
2477
-

-

-
 中1数学まとめ(解説と問題)
中1数学まとめ(解説と問題)0
7006
-

-
 確率の問題と解き方(さいころやくじなど)|中学数学
確率の問題と解き方(さいころやくじなど)|中学数学0
6255
-
 逆比の例と計算(分数、小数、3つ以上の数の比の逆比)|中学数学
逆比の例と計算(分数、小数、3つ以上の数の比の逆比)|中学数学0
18852
-
 中学数学の方程式の文章題攻略法
中学数学の方程式の文章題攻略法0
4091
-

-
 円周の長さから円の半径と直径を計算する|オンライン電卓
円周の長さから円の半径と直径を計算する|オンライン電卓0
10459




