運動量と力積の定義と運動量保存則

物体の運動状態を表すものに運動量という物理量がある。運動量 $p$ は質量と速度の積で定義される。

\[ p = mv \]

例えば $3\text{kg}$ の物質が $4\text{m/s}$ で動いているとき、その物質は $12$ の運動量をもっている。ここで運動量の単位は $kg \cdot m/s$ である（中学理科では扱わない）。重ければ重いほど、または速ければ速いほど運動量は大きくなる。

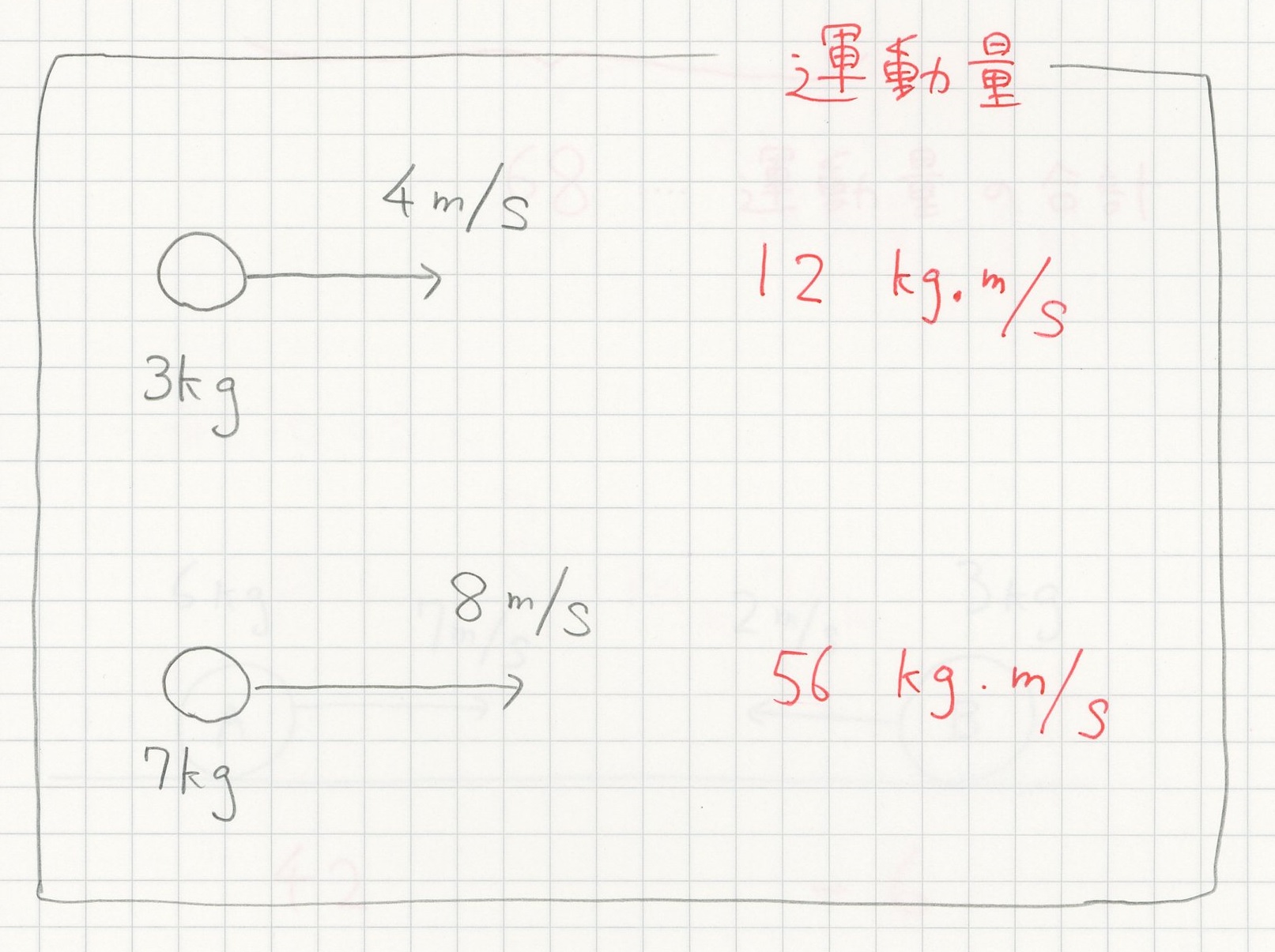
二つの運動量

物質が二つ以上あるとき、全体の運動量はそれぞれの運動量を足したものである。

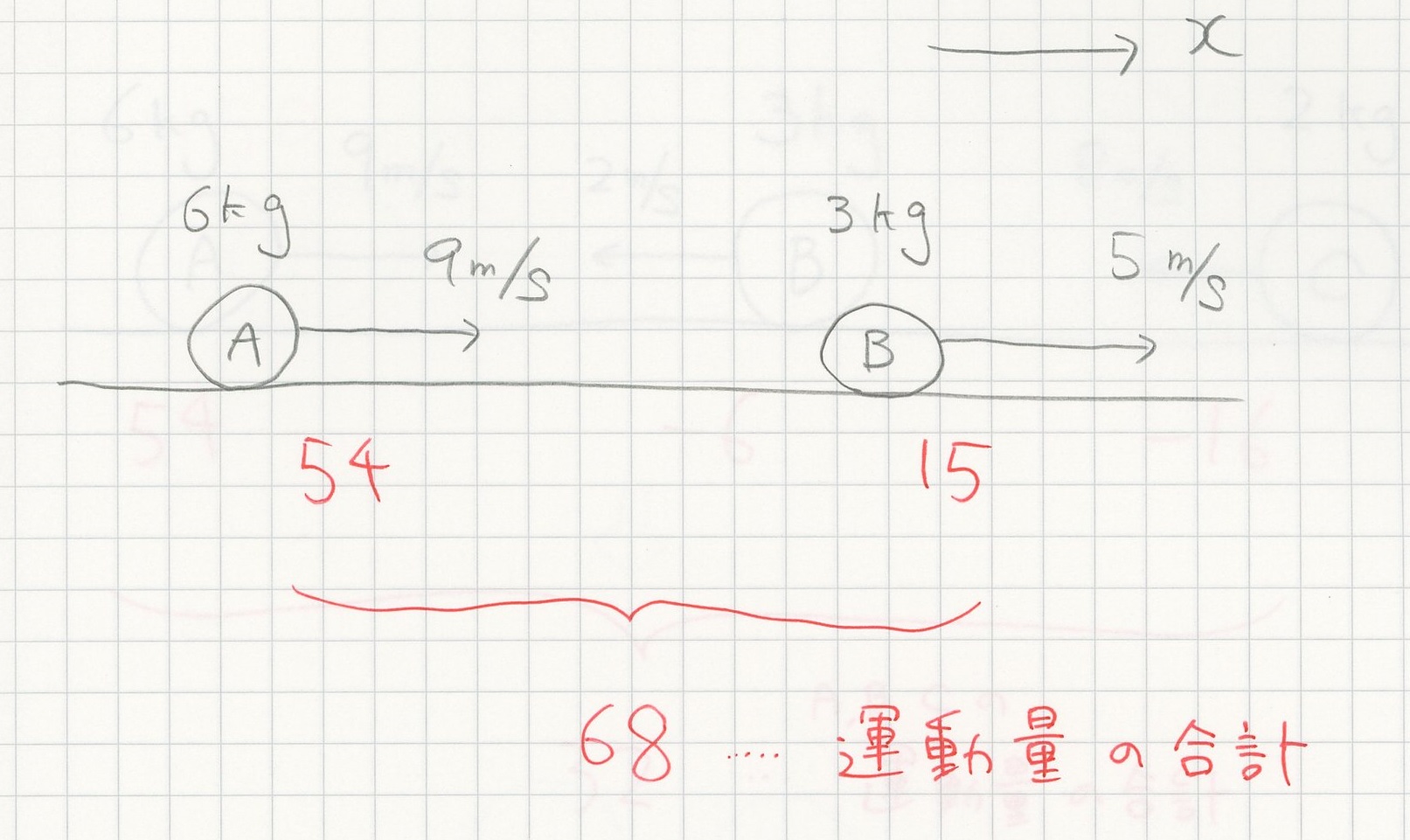
上図の右上に小さく $x$ とあるのは方向である。実は運動量は正負があり、マイナスの方向に動いている物質は負の運動量をもつことになる。

ここで運動量を時間で微分してみよう。

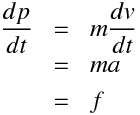
一番上の式において微分を意味する $d$ を $⊿$ にして、一番下の式とつなげると

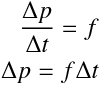
となる。つまり力 $f$ を $⊿t$ という時間だけ与えると、運動量が $⊿p$ だけ変化する。

この $f⊿t$ を力積という。力積とは、物体の受ける力とその力を受けている時間の積であり、運動量の変化である。

上で見たように運動量が変化するときは必ず力が働いている。逆に言えば、外部から力が働かない限りその物体の運動量は変わらない（保存される）。

質量 $m_1$ の物体 1 と質量 $m_2$ の物体 2 がそれぞれ $v_1,\ v_2$ の速度で運動していたとき、全体の運動量は

\[ m_1 v_1 + m_2 v_2 \]

である。ここでこの二つの物体が衝突したとする。衝突すれば互いに力を与え、与えられることになる。そしてこの力はニュートンの作用反作用の法則から絶対値が等しく、向きが逆である。

物体 1 は物体 2 に $f$ 、物体 2 は物体 1 に $-f$ という力を微小時間 $⊿t$ において与えたとする。するとそれぞれの運動量は次のように変化する。

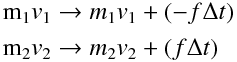
したがって全体の運動量は

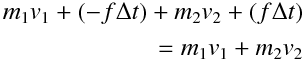
となって変化しない。つまり物体と物体は衝突しても、運動量の合計は保存される。

これは、それぞれの物体は外部から力を与えられているが、全体としては外部から力を与えられていないせいである。なおこのようにいくつかの物体をまとめて考えるとき、そのまとまりを「系」と呼ぶ。

運動量保存則は外部から力が働かない系において全体の運動量の合計が保存されることを示す。

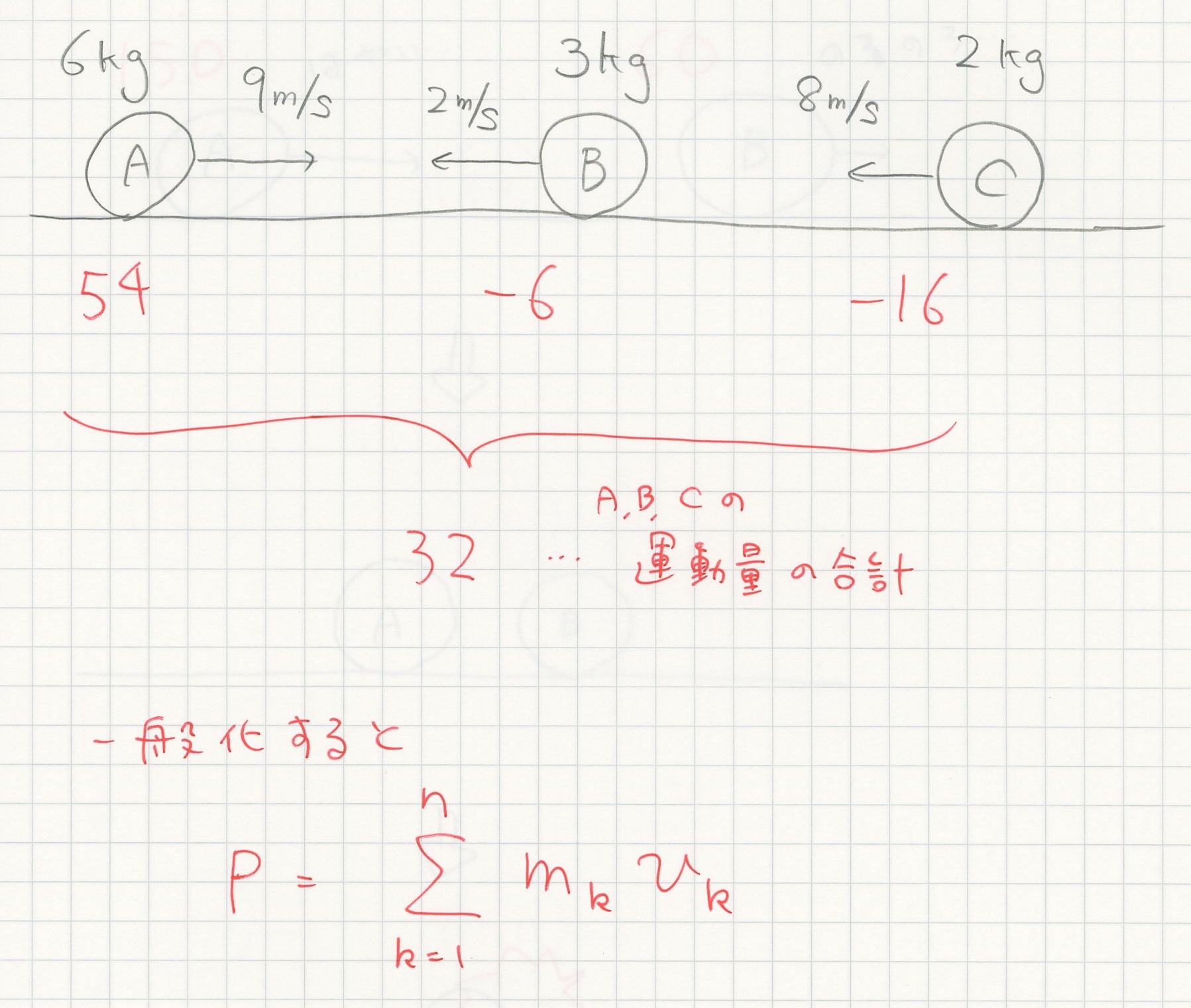
運動量保存則を別の方向から考えてみよう。下図のように 150 の運動量をもつ物質と 60 の運動量をもつ物質があり、衝突して運動量が変わったとする。

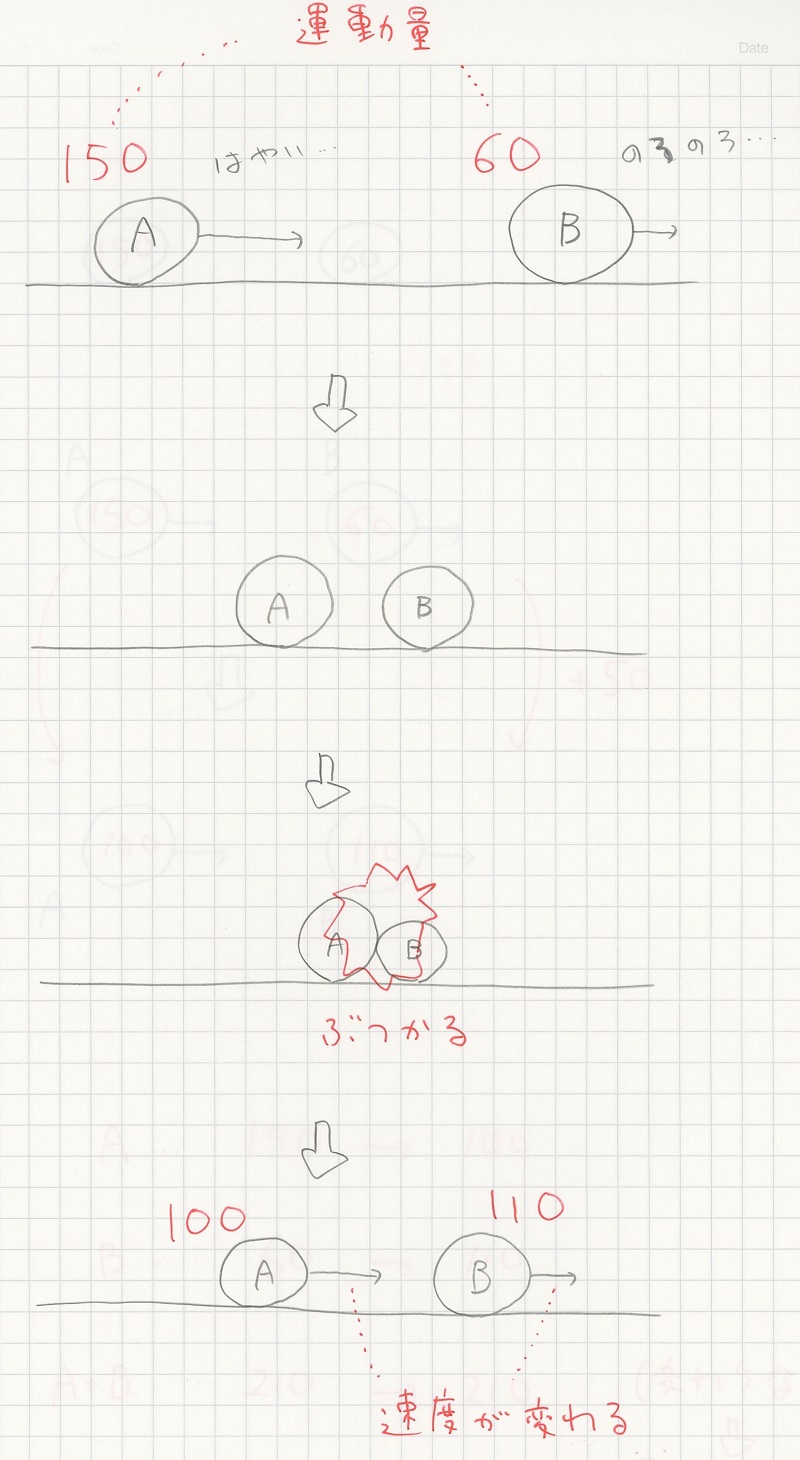
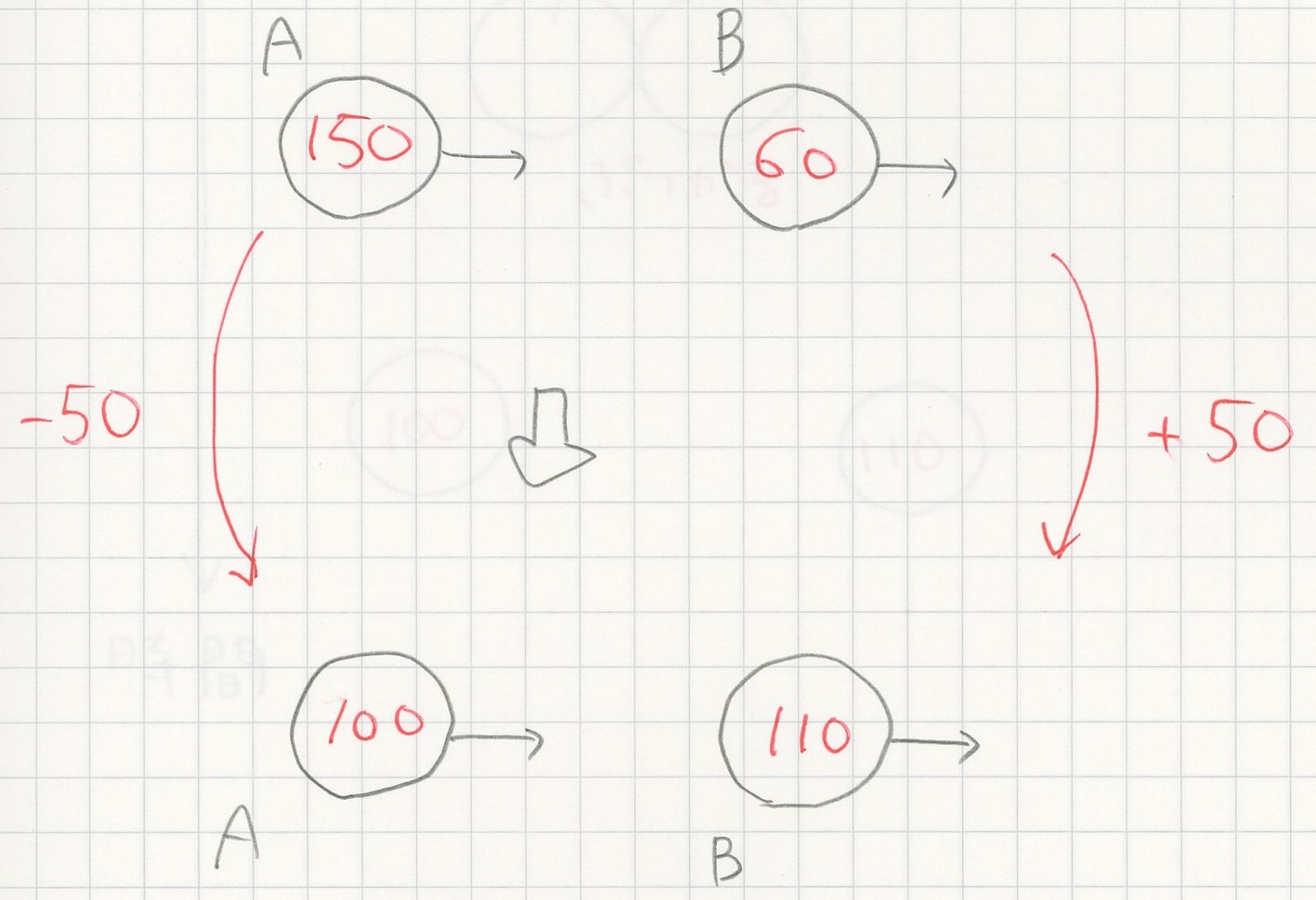
片方がもう片方に運動量を与えている。運動量の一部が移動したことになるが、全体の運動量（運動量の総和）は変わらない。