微分から法線の方程式を求めるやり方：高校数学 2

接線の傾きがわかると法線の方程式もわかります．法線の方程式を求めるときは

1. 導関数
2. その点における微分係数
3. 法線の方程式

の順番に計算します．接線と法線は垂直に交わる線で，その傾きの積は $-1$ です．例えばある点における接線の傾きが $2$ のとき，その点における法線の傾きは

\[ -1 \div 2 = -\frac{ 1 }{ 2 } \]

となります．

例題

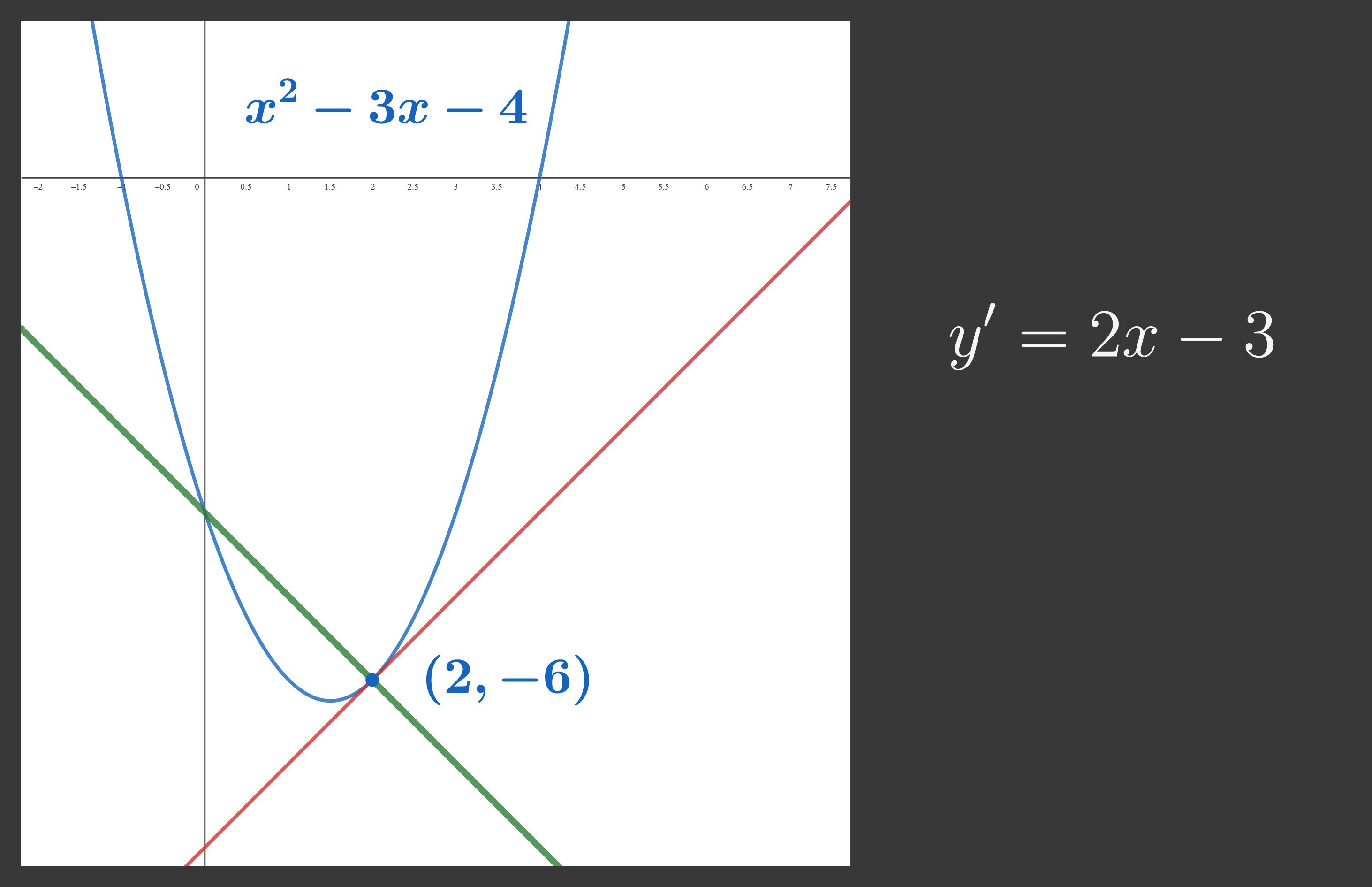
$x^2 - 3x - 4$ の導関数は $2x - 3$ だから，$(2,\ -6)$ における微分係数は

\[ 2 \cdot 2 - 3 = 1 \]

で，接線の傾きは $1$ とわかります．接線と法線の傾きは積が $-1$ になるため，法線の傾きは

\[ -1 \div 1 = -1 \]

となり，法線の方程式は

\begin{split} y &= (-1)(x - 2) - 6 \\ &= -x - 4 \end{split}

$y = -x - 4$ となります．