楕円の方程式と媒介変数表示：円の方程式の一般化

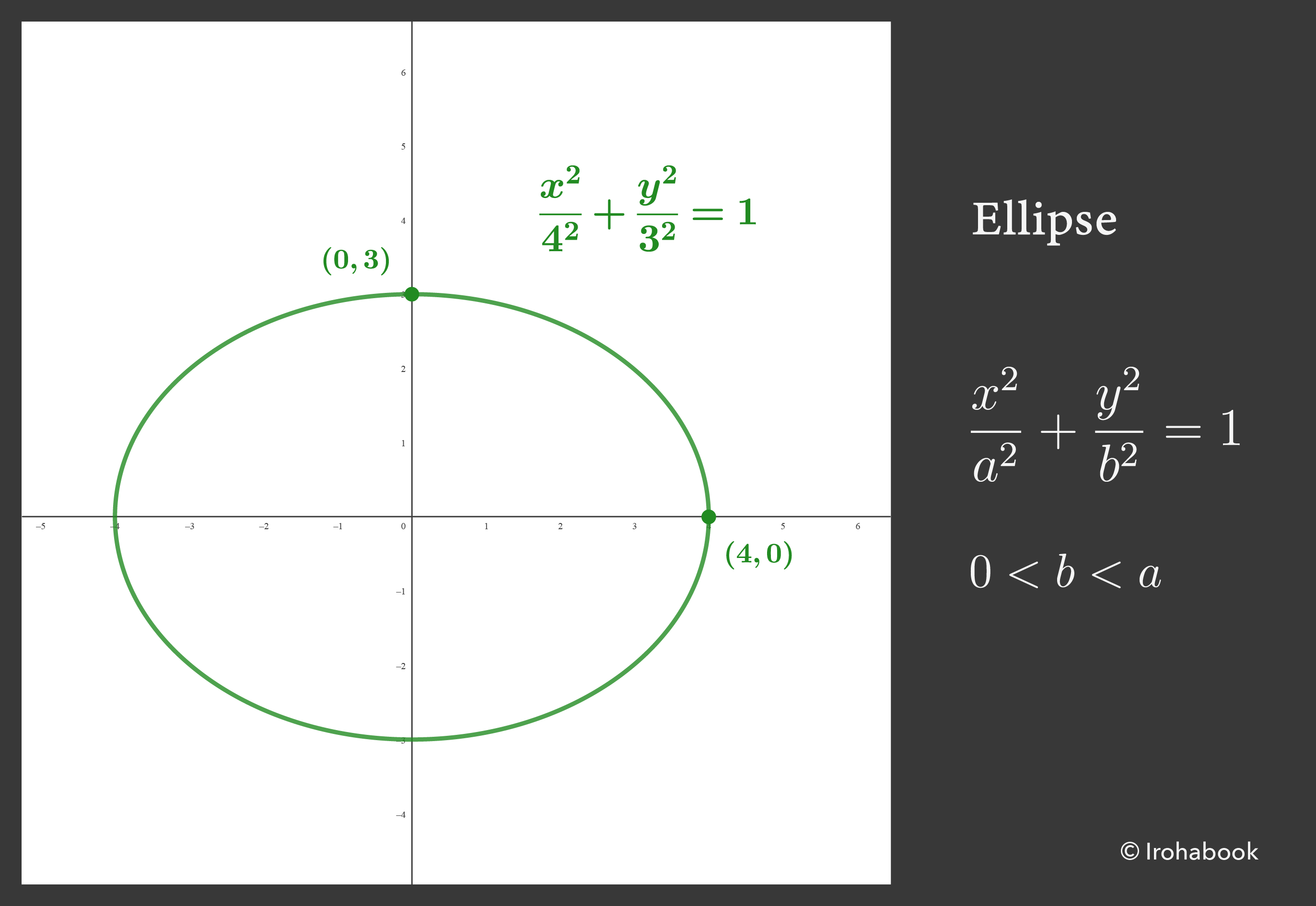
原点を中心とする楕円の方程式は

\[ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \]

です．

円の方程式

\[ \dfrac{x^2}{a^2} + \dfrac{y^2}{a^2} = 1 \]

と似ています．楕円の方程式の $b$ を $a$ にすると円の方程式になり，グラフもちょうど円になります．

楕円の媒介変数表示

\[ \left\{ \begin{array}{l} x = a\cos\theta \\ y = b\sin\theta \end{array} \right. \]