曲線と x 軸にはさまれた領域の面積を計算する - 高校数学 2 定積分

$y = x^2 \ (1 \leqq x \leqq 3)$ と $x$ 軸にはさまれた領域の面積は

\[ S = \int_1^{3} \! x^2 dx \]

です．

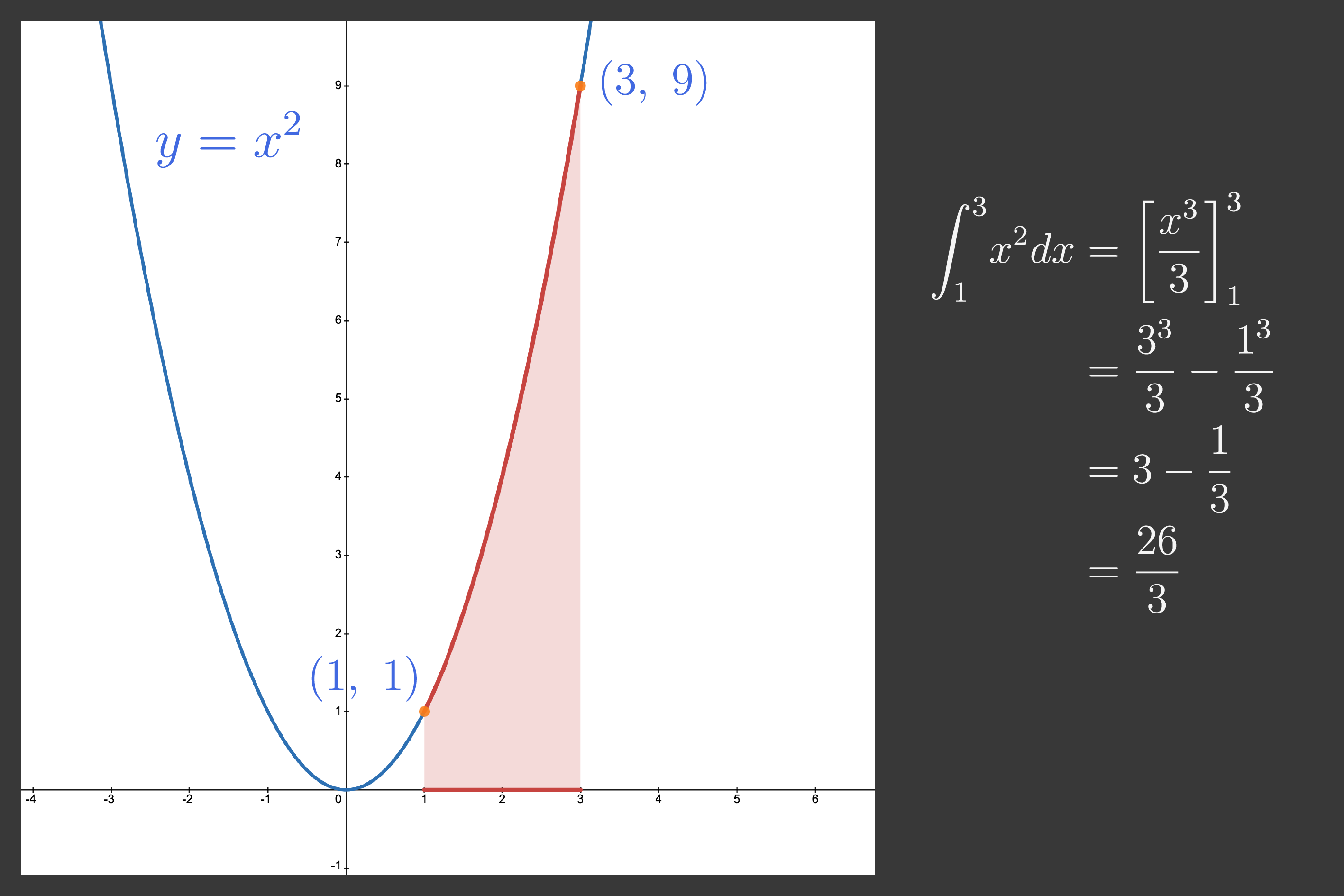
\begin{split} \int_1^{3} \! x^2 dx &= \left[ \frac{ x^3 }{ 3 } \right]^3_1 \\ &= \frac{ 3^3 }{ 3 } - \frac{ 1^3 }{ 3 } \\ &= 3 - \frac{ 1 }{ 3 } \\ &= \frac{ 26 }{ 3 } \end{split}

となり，面積は $\dfrac{ 26 }{ 3 }$ となります．