ルートを分数にできない問題の背理法による証明|高校数学
√2 は q/p と表すことができません。これは背理法というやり方で証明します。
方針
√2 を q/p と表したときに矛盾が出てくることを示す。
ルート 2 を分数にできないことの証明
√2 = q/p とかけるとする。ここで p と q は互いの素の整数である。分数は分子と分母が互いに素になるまで約分できる。
両辺を二乗すると下のように変形できる。
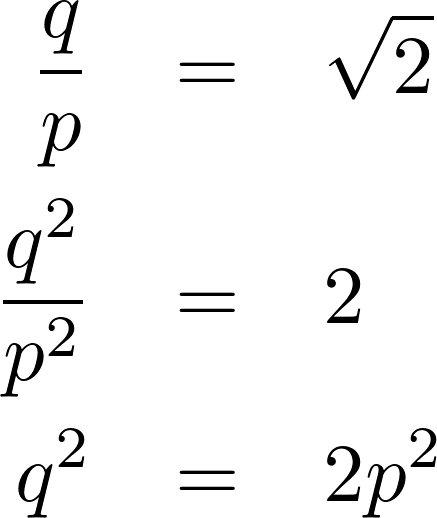
q2 は偶数になる。奇数の二乗は奇数になるので q も偶数になる。すると q = 2n とかける。
q を 2n にすると
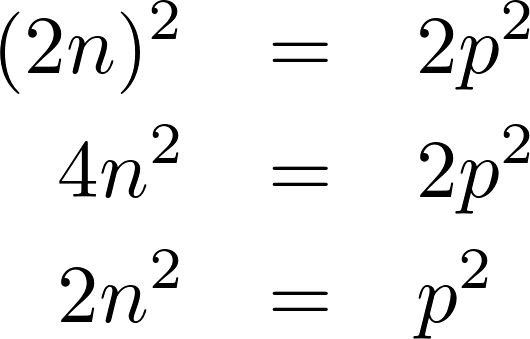
となり、p2 は偶数になる。q のときと同じ理由で p も偶数になる。
p と q は両方とも偶数になることがわかった。これは最初の「p と q は互いに素とする」という仮定に矛盾している。
以上から √2 を q/p と表すことはできないとわかりました。この問題は数学Ⅰの定期試験(中間・期末試験)によく出るので、証明を何度か書いて覚えてみましょう。
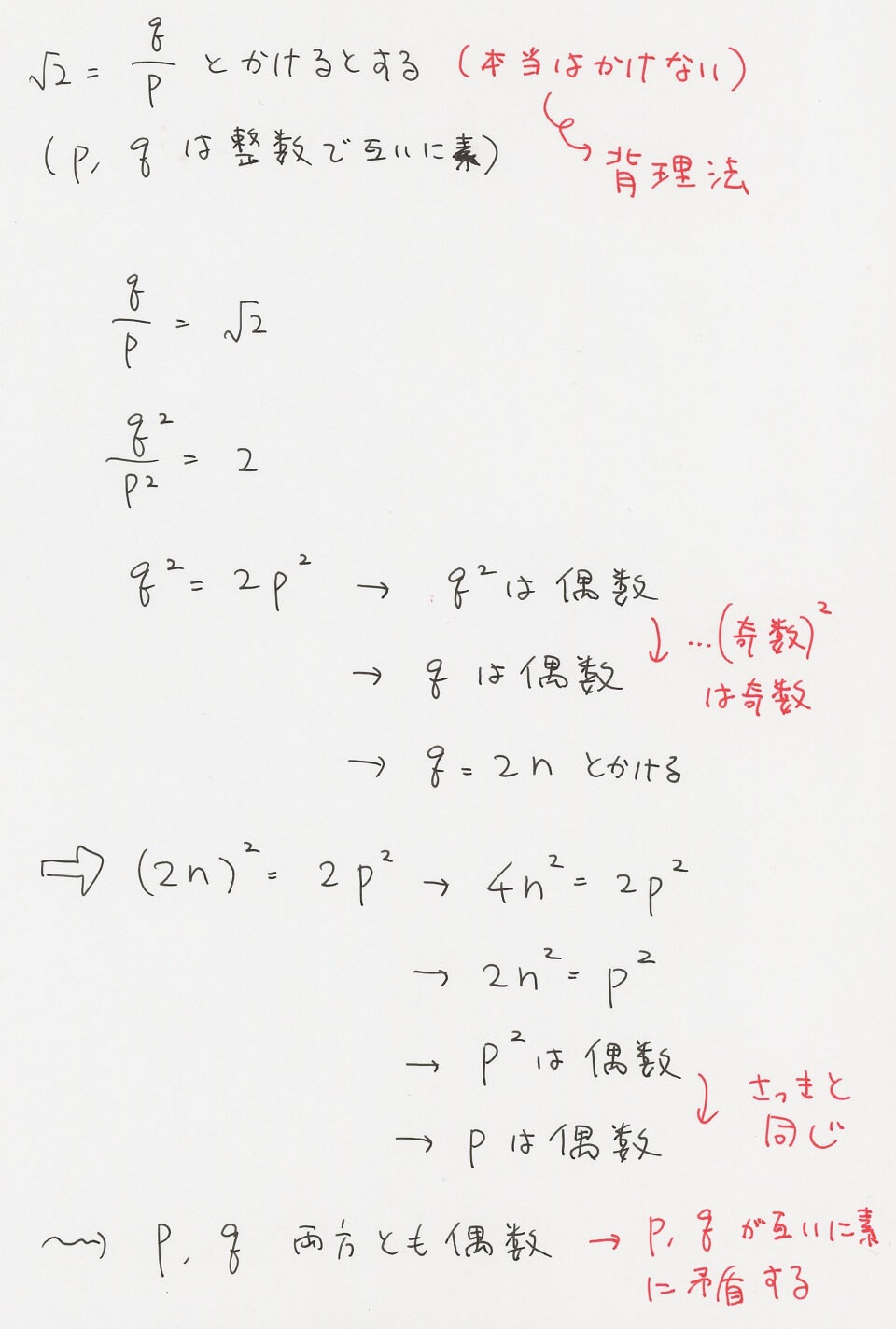
メモ
この問題のポイントは
- 両辺を二乗する
- 奇数の二乗は奇数になる
という点にあります。上の証明で「二乗して偶数になる数は偶数である」とありますが、大学受験ではこれを証明する必要はありません。
TeXコード
\dfrac{q}{p}&=&\sqrt{2}\\
\dfrac{q^2}{p^2}&=&2\\
q^2&=&2p^2
(2n)^2&=&2p^2\\
4n^2&=&2p^2\\
2n^2&=&p^2
集合と命題(数学Ⅰ)

-

-

-

-
 命題の真理値表(否定、かつ、または)
命題の真理値表(否定、かつ、または)0
2891
-
 ルートを分数にできない問題の背理法による証明|高校数学
ルートを分数にできない問題の背理法による証明|高校数学0
2814
-
 命題と条件(「かつ」と「または」、必要条件と十分条件など)
命題と条件(「かつ」と「または」、必要条件と十分条件など)0
11502
-





