三角比の公式まとめ(サイン、コサイン、タンジェント、正弦定理、余弦定理など)
高校数学(数学Ⅰ・図形と計量)で習う三角比の公式をまとめました。サイン、コサイン、タンジェントの基本公式、正弦定理、余弦定理、三角形の面積、直線の傾きなどを確認してください。
三角比の定義
a、b、cを辺とする直角三角形(高さがa、底辺がb、斜辺がc、底辺と斜辺のなす角をθ)で三角比を次のように定義します。
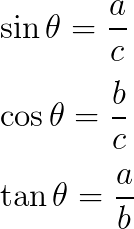
\sin\theta=\frac{a}{c}\\
\cos\theta=\frac{b}{c}\\
\tan\theta=\frac{a}{b}
三角比の定義を正確に覚えましょう。まずは sin と cos の定義を覚えてください。それから tan の式を覚えます。
よくサイン・コサイン・タンジェントといいますが、タンジェントは特別です。タンジェントは接線という意味もあり、本質は三角比よりも曲線の接線にあります。サイン・コサインとタンジェントは完全な別物と認識してください。
三角比の基本公式
sin/cos がタンジェントになる式と、sin の 2 乗と cos の 2 乗の和が 1 になる公式があります。これを三角比の基本公式といいます。
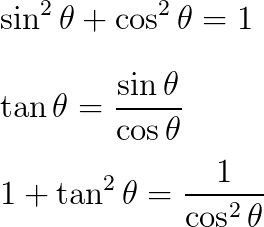
\sin^{2}\theta+\cos^{2}\theta=1\\
\tan\theta=\frac{\sin\theta}{\cos\theta}\\
1+\tan^{2}\theta=\frac{1}{\cos^{2}\theta}
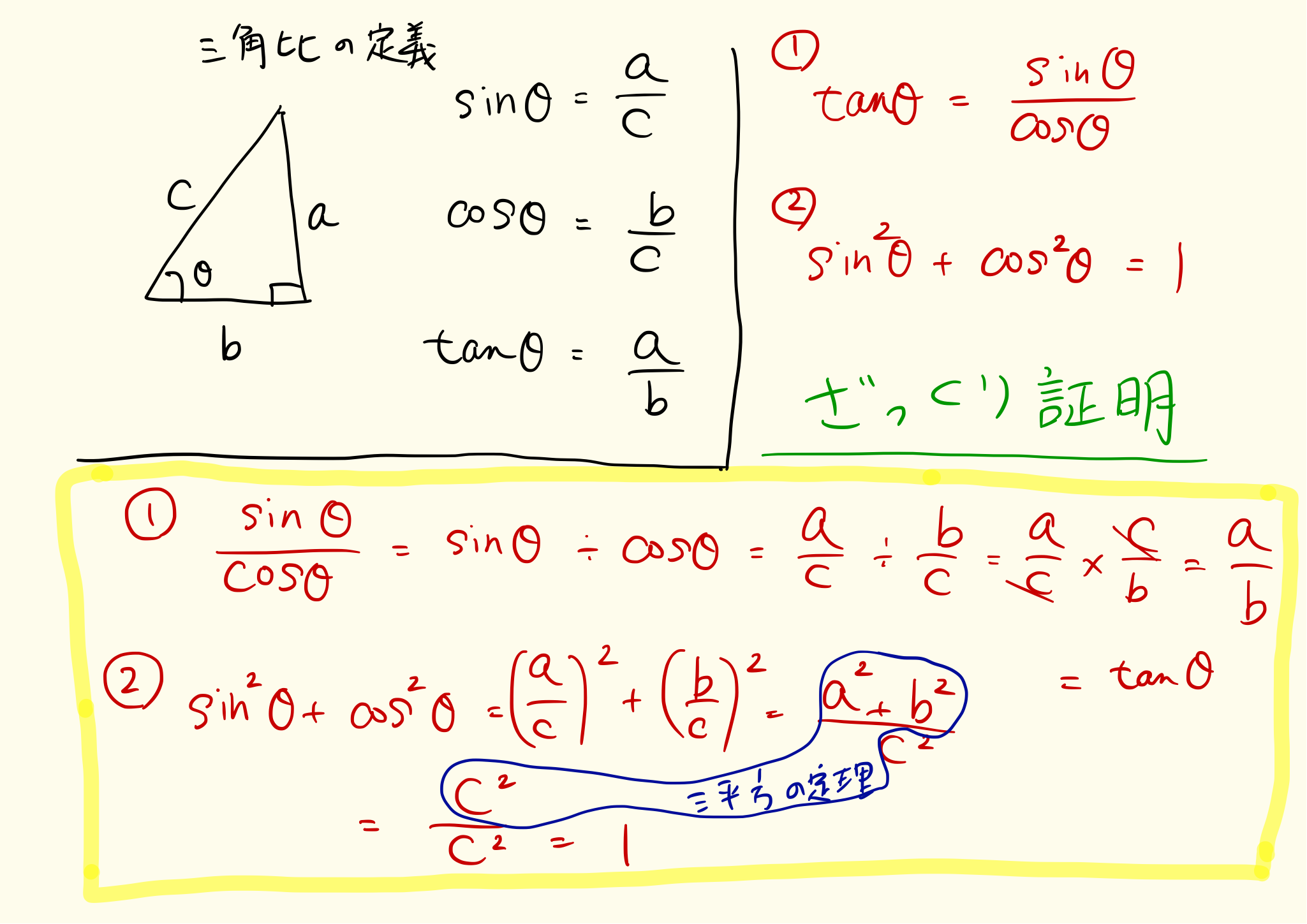
三角比の公式はほぼすべて三角比の基本公式を基礎にしています。三角比が苦手な人は基本公式を使った計算問題をくりかえし解きましょう。三角比の難しさはサイン・コサインのわかりにくい概念にあり、公式そのものはそこまで複雑ではない。三角比を得意にするには、単純な計算問題を解いてひたすら慣れていくしかない。
三角比の 90°- 公式
三角比 90°− はわかりにくい公式で、最初は使いみちも理解しにくい。
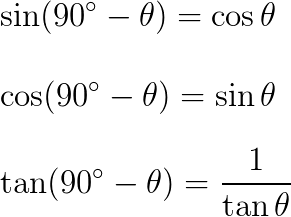
\sin(90^{\circ}-\theta)=\cos\theta\\
\cos(90^{\circ}-\theta)=\sin\theta\\
\tan(90^{\circ}-\theta)=\frac{1}{\tan\theta}
例えば cos 15° を求めたいとき、上の公式を使うと sin 75° に等しいことがわかる。つまりこの公式は cos と sin の関係を表しています。難しい問題ではよく cos と sin の相互変換が出てくるため、この三角比 90° −は頻繁に使います。
試験では tan の公式をパッと使えるかどうかで差がつきます。公式を見てください。tan だけ分数になっていて、少しとっつきにくい印象がありますね。実際ここで三角比の試験は差がつくので、必ずおさえておきましょう。
三角比の 90°+ 公式
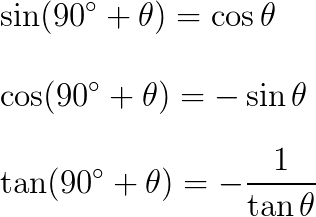
\sin(90^{\circ}+\theta)=\cos\theta\\
\cos(90^{\circ}+\theta)=-\sin\theta\\
\tan(90^{\circ}+\theta)=-\frac{1}{\tan\theta}
三角比 90° +の公式もよく使います。例えば cos 120° は三角比 90° +の公式から sin 30° に等しいとわかります。上の公式と同じように tan は複雑な印象があり、やはり試験で差がつきます。
三角比の 180°- 公式
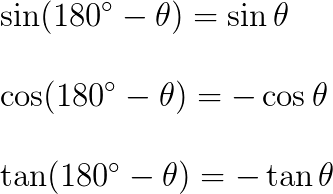
\sin(180^{\circ}-\theta)=\sin\theta\\
\cos(180^{\circ}-\theta)=-\cos\theta\\
\tan(180^{\circ}-\theta)=-\tan\theta
この公式は上の 90° と比べるとそこまで重要ではないかもしれません。
正弦定理
△ABCの3辺をそれぞれa=BC、b=CA、c=ABとして、三角形の外接円の半径をRとします。このとき次の公式(正弦定理)が成り立ちます。
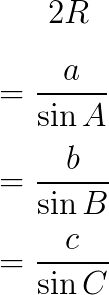
\begin{eqnarray*}
2R&=&\frac{a}{\sin{A}}\\
&=&\frac{b}{\sin{B}}\\
&=&\frac{c}{\sin{C}}
\end{eqnarray*}
正弦定理は下のように変形してもかまいません。
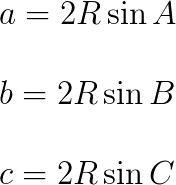
a=2R\sin{A}\\
b=2R\sin{B}\\
c=2R\sin{C}
三角比で最も重要な公式の一つが、この正弦定理の公式です。正弦定理は定期試験ではもちろん、大学受験でも高確率で出てきます。三角比といったら正弦定理と余弦定理です。そして正弦定理は上二つの変形ができるかできないかで差がつきます。この記事を読んだらすぐに、両者が等価な式であることを確認しましょう。
正弦定理は動画でくわしく説明しました(動画は年内に削除されます)。
余弦定理
△ABCの3辺をそれぞれa=BC、b=CA、c=ABとします。このとき次の公式(余弦定理)が成り立ちます。余弦定理の「余弦」は「よげん」と読みます。
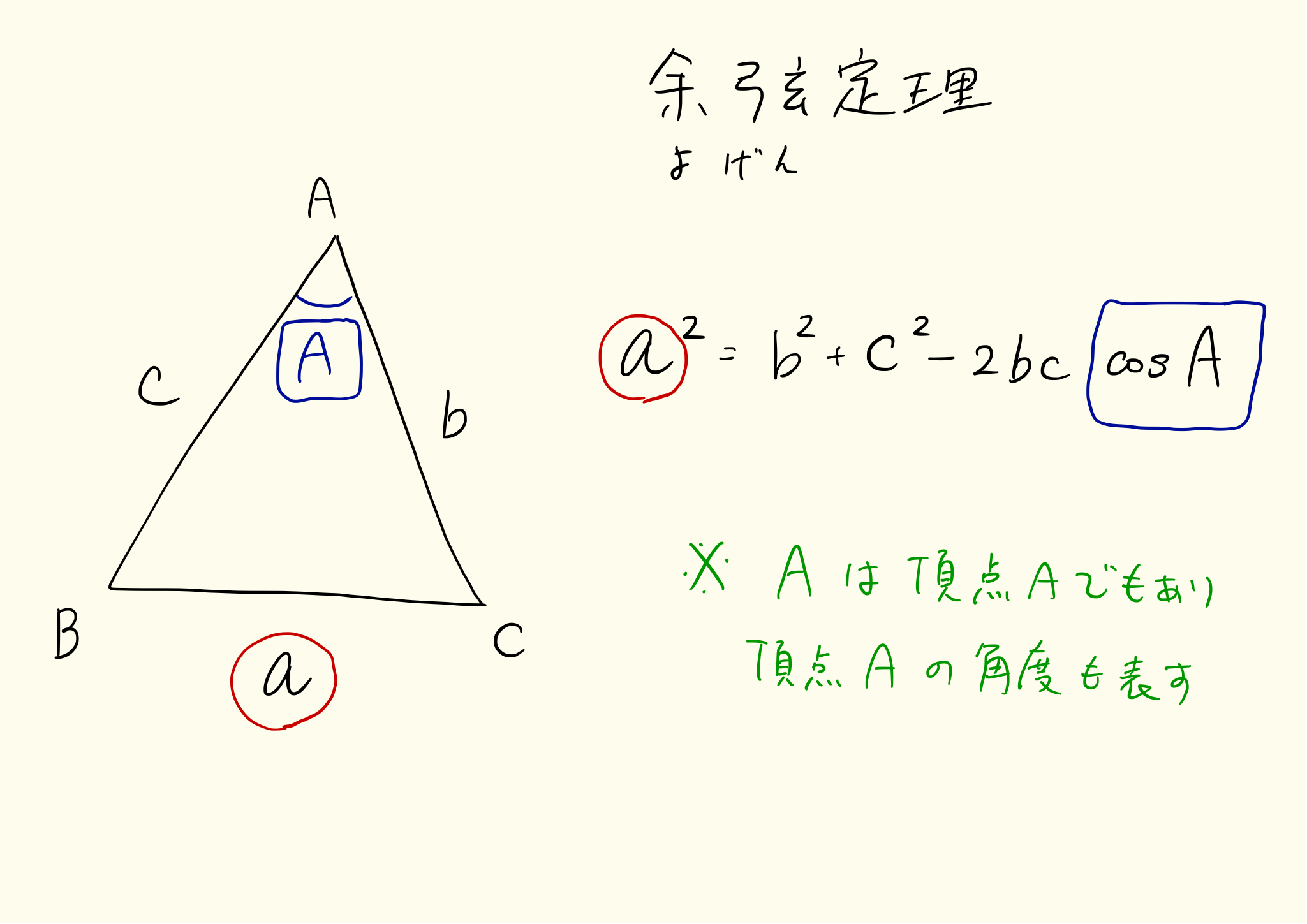
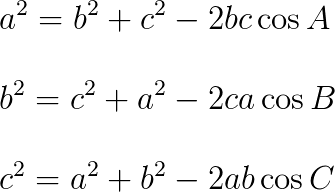
a^{2}=b^{2}+c^{2}-2bc\cos{A}\\
b^{2}=c^{2}+a^{2}-2ca\cos{B}\\
c^{2}=a^{2}+b^{2}-2ab\cos{C}
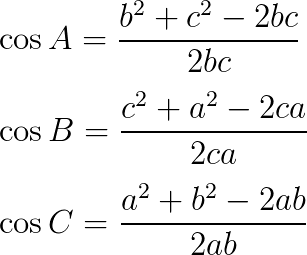
\cos{A}=\frac{b^{2}+c^{2}-2bc}{2bc}\\
\cos{B}=\frac{c^{2}+a^{2}-2ca}{2ca}\\
\cos{C}=\frac{a^{2}+b^{2}-2ab}{2ab}
余弦定理は正弦定理と同じく三角比を代表する定理。こちらも相互変換がきちんとできるようにしましょう。上と下のどちらも使います。
余弦定理の最初の式を見てください。式から -2bc\cos{A} の部分を消すと a^{2}=b^{2}+c^{2} となりますが、これは三平方の定理そのものですね。つまり余弦定理とは三平方の定理の拡張なのです。
むしろ三角比は三平方の定理を拡張するための道具として機能するともいえます。
三角形の面積
△ABCの3辺をそれぞれa=BC、b=CA、c=AB、面積をSとします。
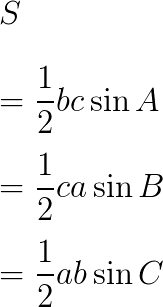
\begin{eqnarray*}
S&=&\frac{1}{2}bc\sin{A}\\
&=&\frac{1}{2}ca\sin{B}\\
&=&\frac{1}{2}ab\sin{C}
\end{eqnarray*}
二辺の長さと、その辺にはさまれた角度がわかっているときに公式を使います。これは底辺×高さ÷2という公式の応用とみなすことができます。
次の三角形の面積を求めてみましょう。
(1) b=4、c=5、A=30°
(2) b=6、c=2、A=60°
(1)
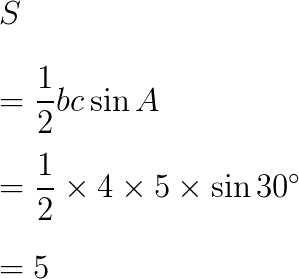
(2)
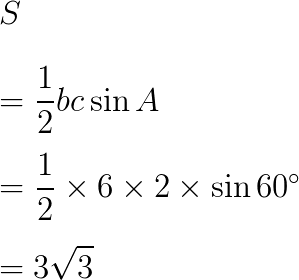
S
=\frac{1}{2}bc\sin{A}\\
=\frac{1}{2} \times 4 \times 5 \times \sin{30^\circ}\\
=5
S
=\frac{1}{2}bc\sin{A}\\
=\frac{1}{2} \times 6 \times 2 \times \sin{60^\circ}\\
=3\sqrt{3}
直線の傾き
三角比の単元であまり目立ちませんが、直線の傾きを tanθ で記述することができます。
直線 $y=ax+b$ とx軸(の正の向き)のなす角をθとすると
\[ a = tanθ \]
となります。これは地味に重要ポイントで、数学Ⅰなどの他単元とからめて出題されます。
三角比の公式に慣れるコツ
三角比の計算問題をコツコツとやってみましょう。そうすると 90° 公式を嫌でも使うようになります。あの公式は演習問題をやっていくうえで不可欠な公式なのです。
最初にうまく慣れたら、正弦定理と余弦定理はそこまで難解に感じないでしょう。しかし変換が重要で、問題に合わせて合った式を使うことがちょっと大変。いずれにせよ、三角比はただぼうっと公式を眺めてもしょうがなく、ひたすら計算して地道に慣れることが大事です。
参考
三角比(数学Ⅰ)

-
 わかりやすい三角比と基本公式
わかりやすい三角比と基本公式0
365092
-
 三角比の正弦定理の公式
三角比の正弦定理の公式0
3339
-

-





