平方根（ルート）の足し算と引き算のやり方と計算問題（中学3年生数学）

根号（ルート）の中が同じの時，平方根は足したり引いたりできる．

\[ \sqrt{2} + \sqrt{2} = 2\sqrt{2} \\ \sqrt{3} + 5\sqrt{3} = 6\sqrt{3} \\ 3\sqrt{7} + 2\sqrt{7} = 5\sqrt{7} \\ 4\sqrt{2} - 2\sqrt{2} = 2\sqrt{2} \\ -5\sqrt{3} + 2\sqrt{3} = -3\sqrt{3} \\ -2\sqrt{5} - (-4\sqrt{5}) = 2\sqrt{5} \]

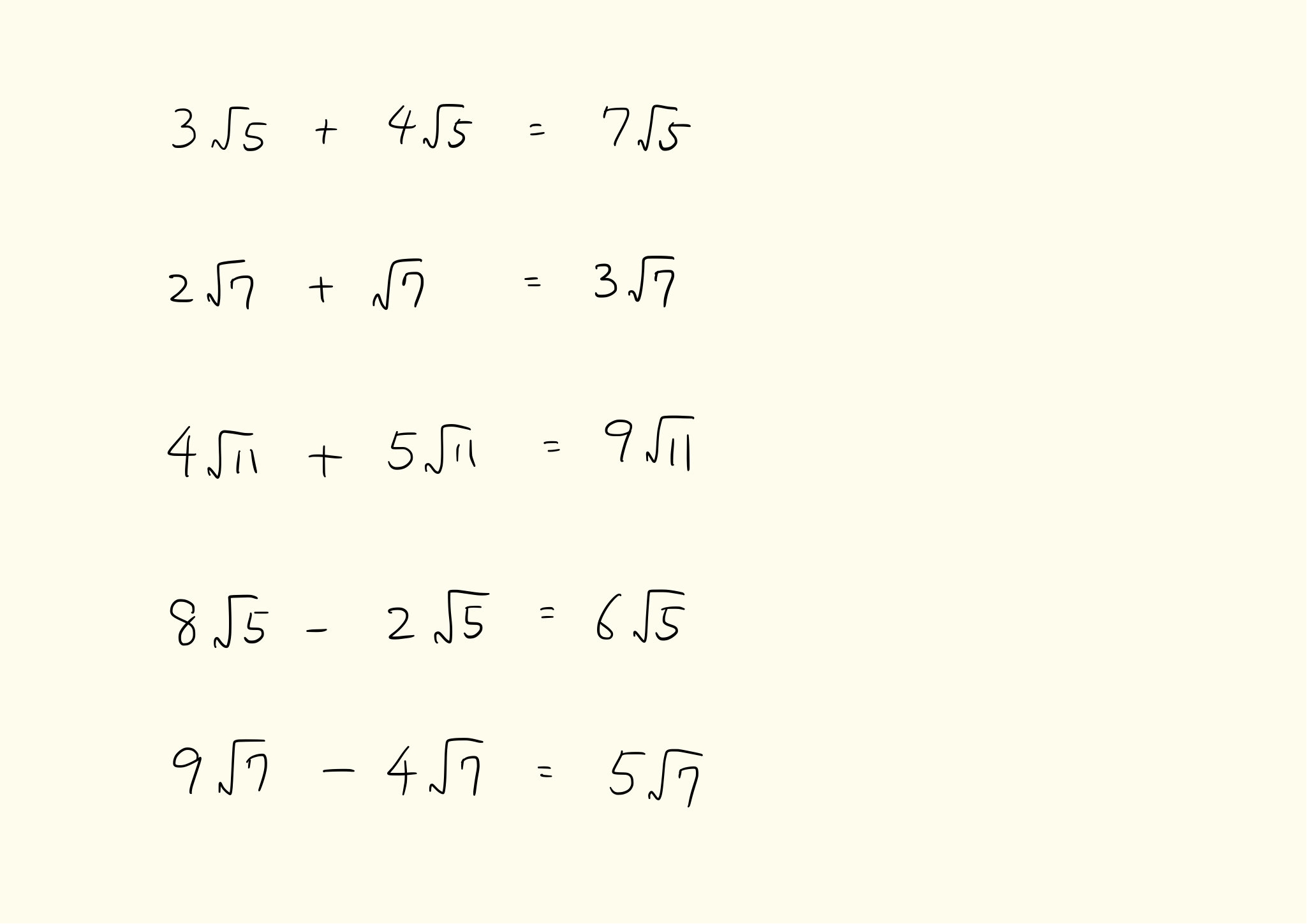
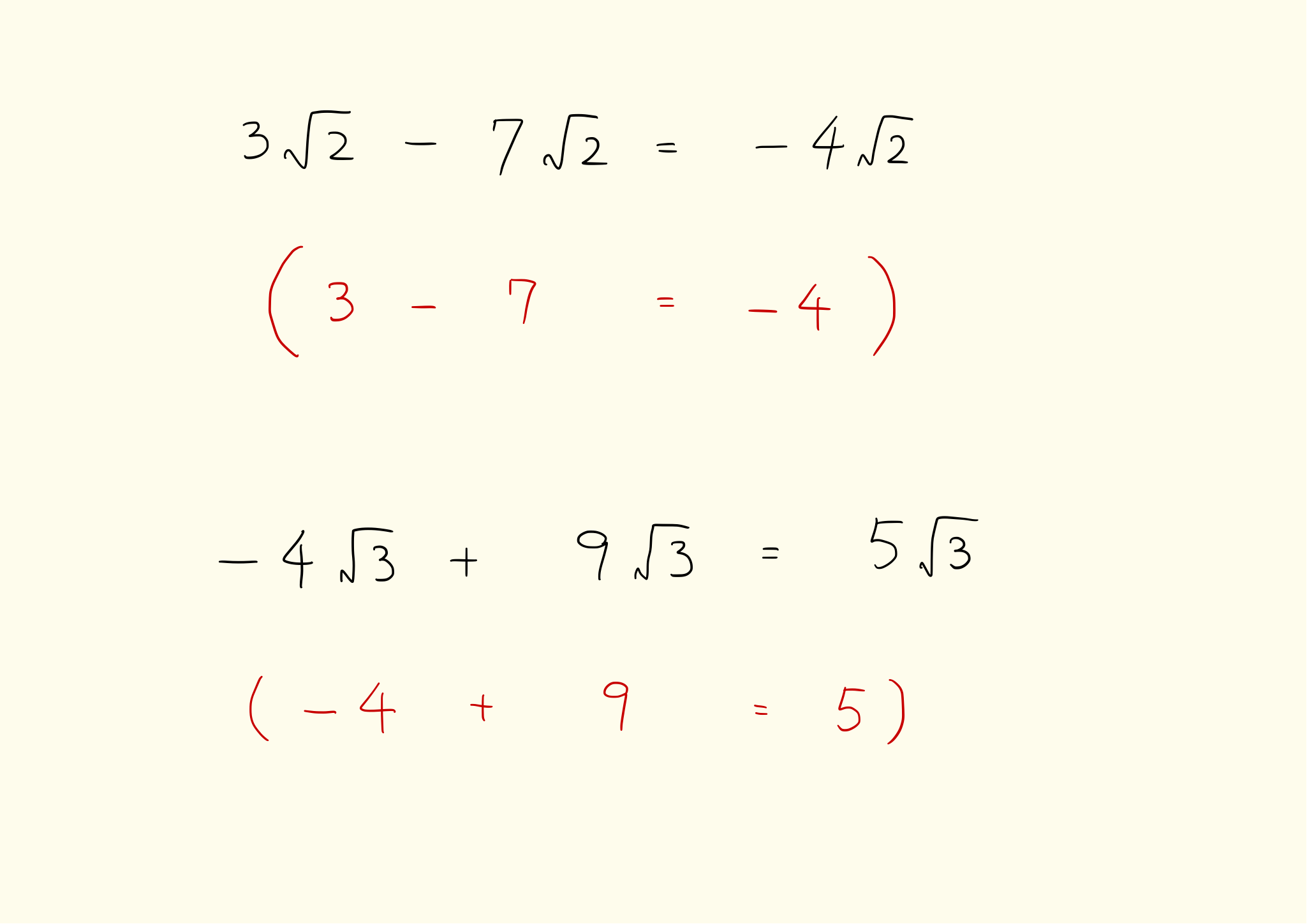
平方根の中身が異なる場合

ルートの中身が異なる場合，そのままの形では足し算と引き算はできない．下図のポイントにあるように，平方根の中身をそろえてから足し算・引き算をします．

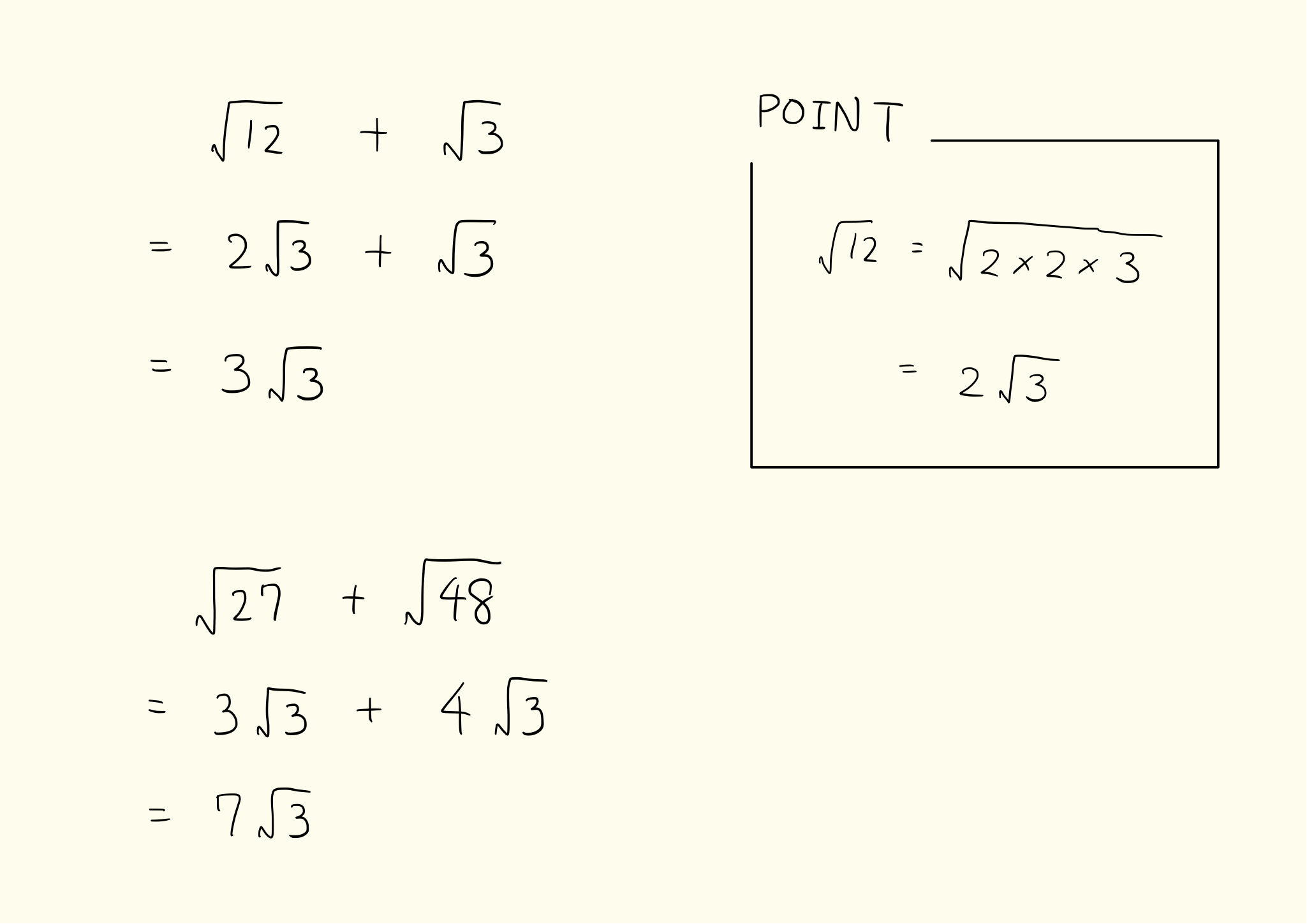
\[ \sqrt{12} + \sqrt{3} = 2\sqrt{3} + \sqrt{3} = 3\sqrt{3} \\ \sqrt{27} + \sqrt{48} = 3\sqrt{3} + 4\sqrt{3} = 7\sqrt{3} \\ \sqrt{50} + \sqrt{8} = 5\sqrt{2} - 2\sqrt{2} = 3\sqrt{2} \\ \sqrt{45} + \sqrt{20} = 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5} \\ -\sqrt{2} + \sqrt{72} = -\sqrt{2} + 6\sqrt{2} = 5\sqrt{2} \\ -\sqrt{28} + \sqrt{7} = -2\sqrt{7} + \sqrt{7} = -\sqrt{7} \]