球の体積と表面積（公式と計算問題と証明）

中学1年生の3学期で球の体積と表面積を習います。球の半径をrとすると、体積と表面積は次のように求めます。

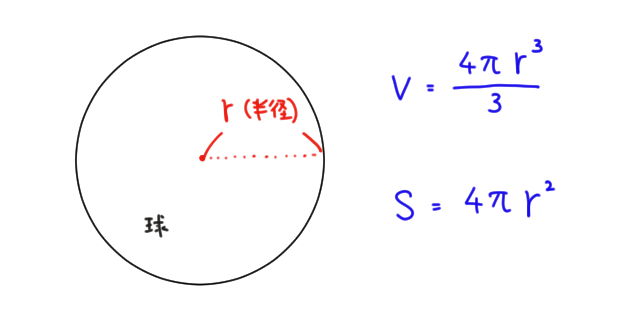
体積の公式

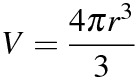
「身の上心配アール３乗」と覚える。

表面積の公式

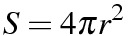
「心配アール２乗」と覚える。

問題

(1)　半径 1cm の球の体積と表面積は求めなさい。

(2)　半径 2cm の球の体積と表面積は求めなさい。

(3)　半径 3cm の球の体積と表面積は求めなさい。

(4)　半径 4cm の球の体積と表面積は求めなさい。

(5)　半径 6cm の球の体積と表面積は求めなさい。

解答

(1)

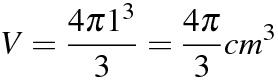
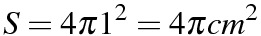
(2)

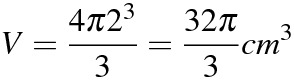
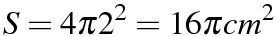
(3)

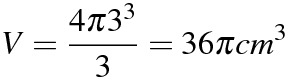
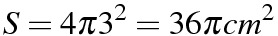
(4)

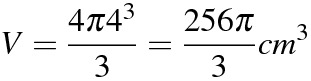
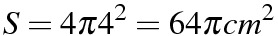
(5)

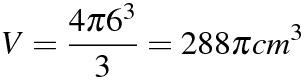
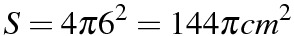
半径3cmの球の体積と表面積は等しい。

補足

上の練習問題で、半径が2cmの球は半径が1cmの球に比べて、体積は8倍、表面積は4倍になっています。

• 半径が2倍になると、体積は8倍になる。
• 半径が2倍になると、表面積は4倍になる。

同じように

• 半径が3倍になると、体積は27倍になる。
• 半径が3倍になると、表面積は9倍になる。

となります。

球の体積は球をすっぽりつつむ円柱の体積の2/3倍

半径rの球がちょうど入る円柱を考えます。これは半径rの円を底面とする、高さが2rの円柱です。缶詰の中に野球ボールがあるようなイメージです。実はこの野球ボールの体積は缶詰の体積の2/3倍です。

円柱の体積

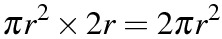
球の体積

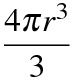
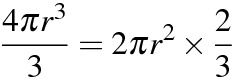
となります。

球の体積を証明する（高校以上）

球は半円を（直径を軸として）回転させた図形です。球を単位円の上半分

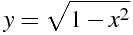
をx軸を軸として回転させた図形と考えます。球の体積をVと書くことにすると

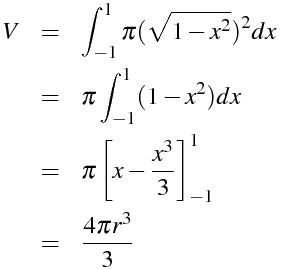
となります。

球の表面積の証明

球の表面積は球の体積から求められます。感覚的な議論になりますが、立体図形を理解する上で重要なポイントが出てきます。

球を「球の中心を頂点とする円錐」の集まりとみなすと、球の体積は球の表面積に半径をかけて3で割った値になります。なぜなら円錐の体積は底面と高さをかけて3で割って求めるからです。

球の体積は

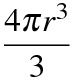
であるため、球の表面積をSとすると

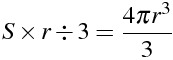
となり

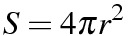
という公式が導かれます。この考え方は立方体にも通用します。立方体の半径をrとすると

立方体の体積 = r³
立方体の表面積 = 6r²

となります。一方、立方体は「立方体の中心を頂点、立方体の各面を底面とする四角錐」に分割できることから、立方体の体積は立方体の表面積にr/2をかけて3で割った値になるはずです。

6r² × r/2 ÷ 3 = r³

となりもともとの値と一致しました。