命題と条件（「かつ」と「または」、必要条件と十分条件など）

高校数学Ⅰの命題と条件について解説します。命題と条件、特に必要条件と十分条件はセンターの数学で必ず出るところです。この記事を読んでぜひ理解してください。

条件はpやqという記号で表します。例えば「雨が降ったら傘をさす」は「雨が降る」と「傘をさす」の二つがくっついた文です。この二つを条件といいます。「雨が降る」をp、「傘をさす」をqとすると

p→q

となります。この文を命題といいます。

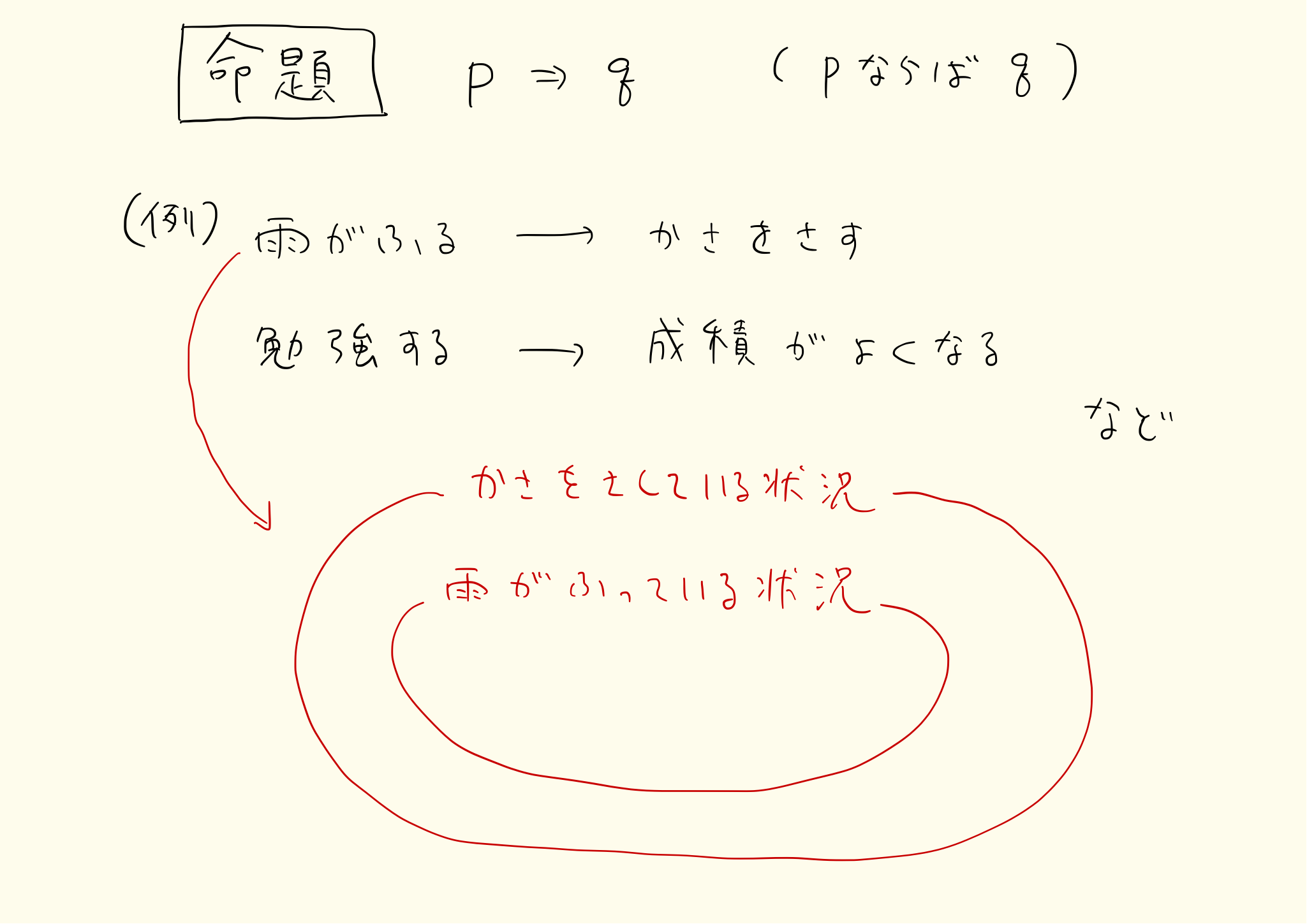
二つの条件が→でつながったものが命題です。

かつとまたは

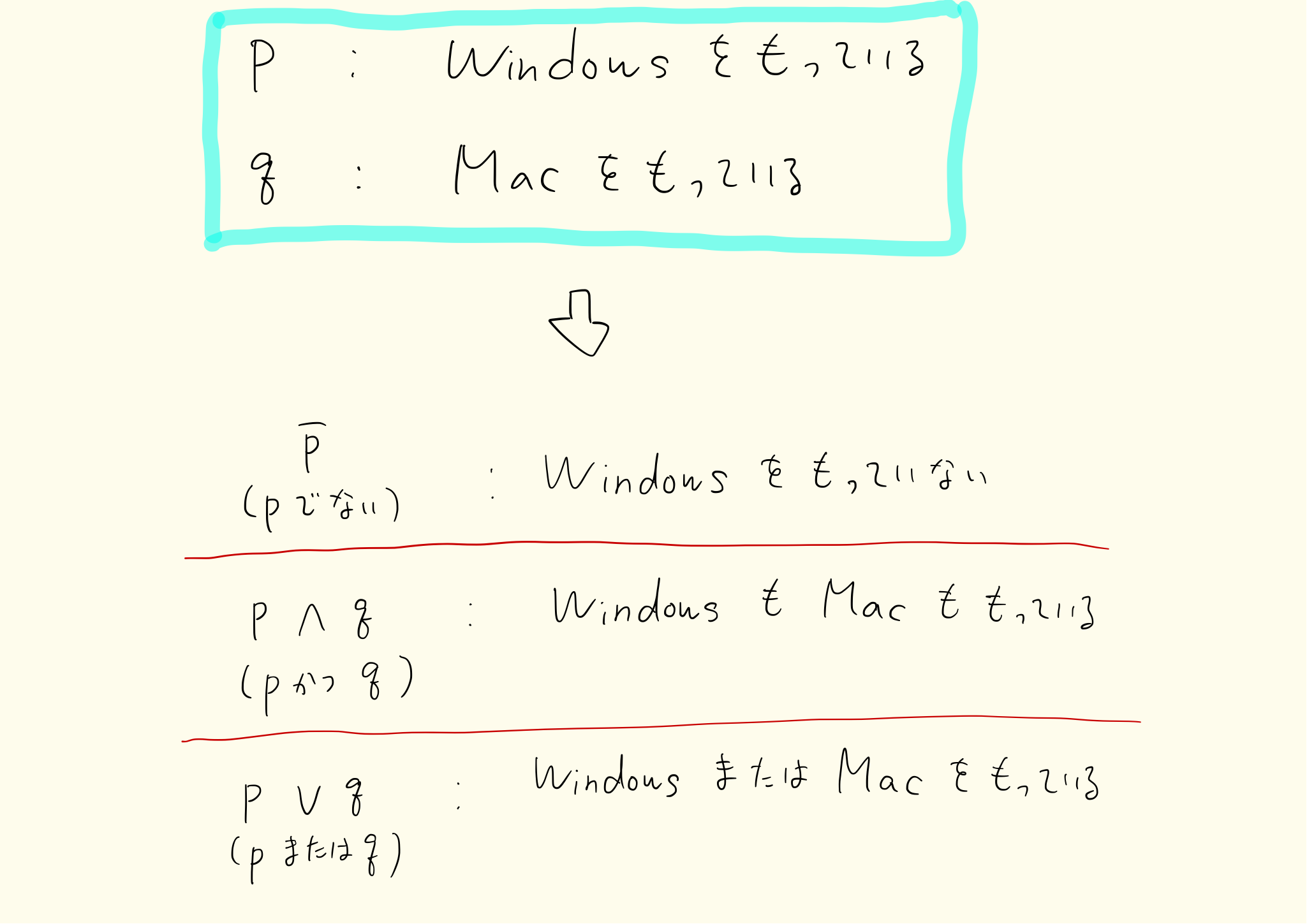
pとqをそれぞれ「Windowsを持っている」「Macを持っている」とします。このときpでない、pかつq、pまたはqは上図のようになります。

pでない…Windowsを持っていない
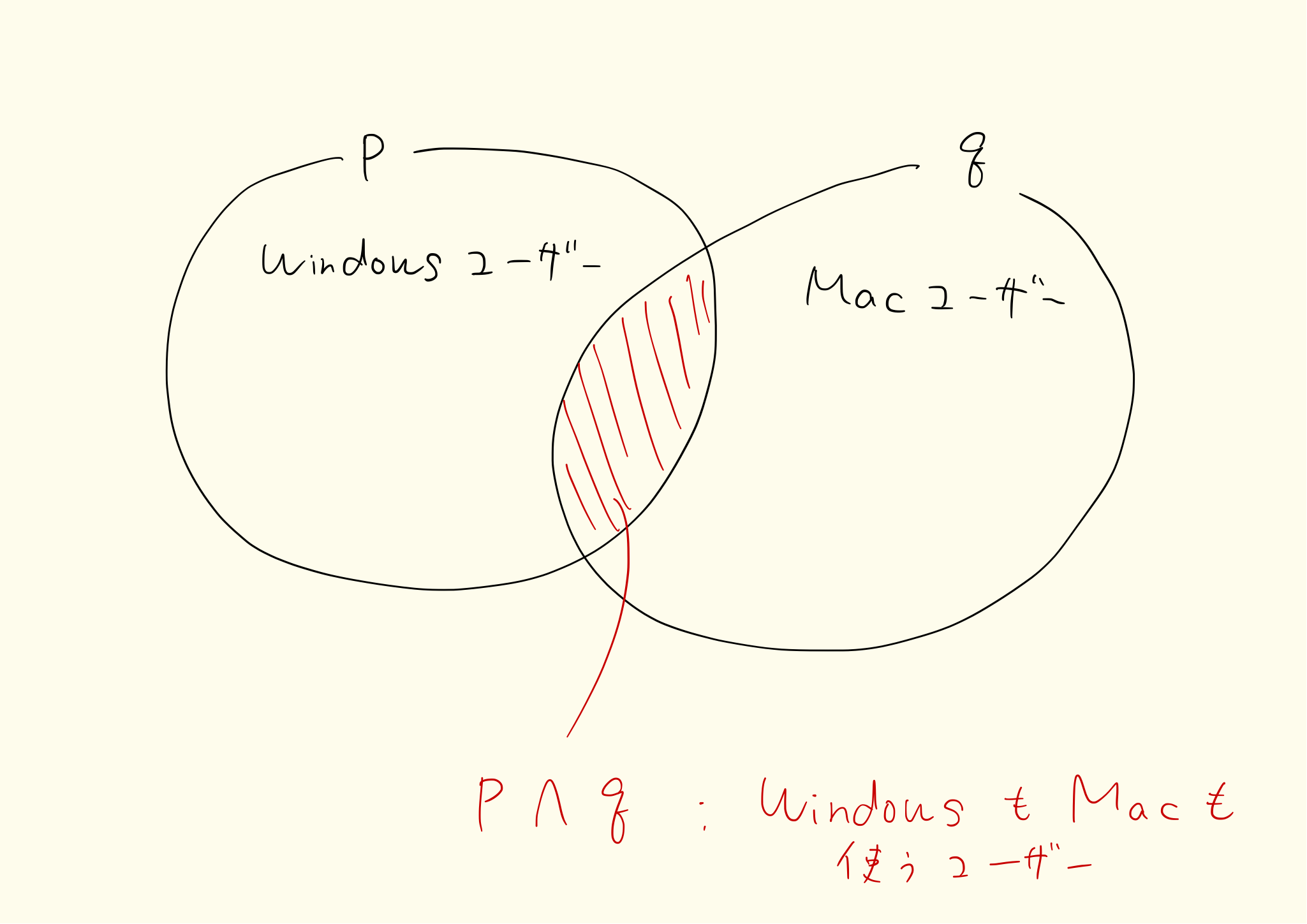
pかつq…両方持っている
pまたはq…どちらかは必ず持っている

pかつqはわかりやすいと思いますが、pまたはqは少しわかりにくいかもしれません。pまたはqは最低限どちらかを持っているという意味です。両方持っている人もこれに当たります。つまりpまたはqはpかつqを含んだ概念です。

p→qが真実のとき、qはpであるための必要条件といいます。逆にpはqであるための十分条件といいます。

下図の例を見て感覚をつかみましょう。

x^2＞1はx＞Ⅰであるための必要条件です。しかしx^2＞1はx＞Ⅰであるための十分条件ではありません。図にあるようにx=-1といった例があるからです。命題は、少しでも例外があったら真実といえません。間違いであることを示す例を反例といいます。この場合はx=-1が反例です。

p→qもq→pも正しいとき、qはpであるための必要十分条件といいます。

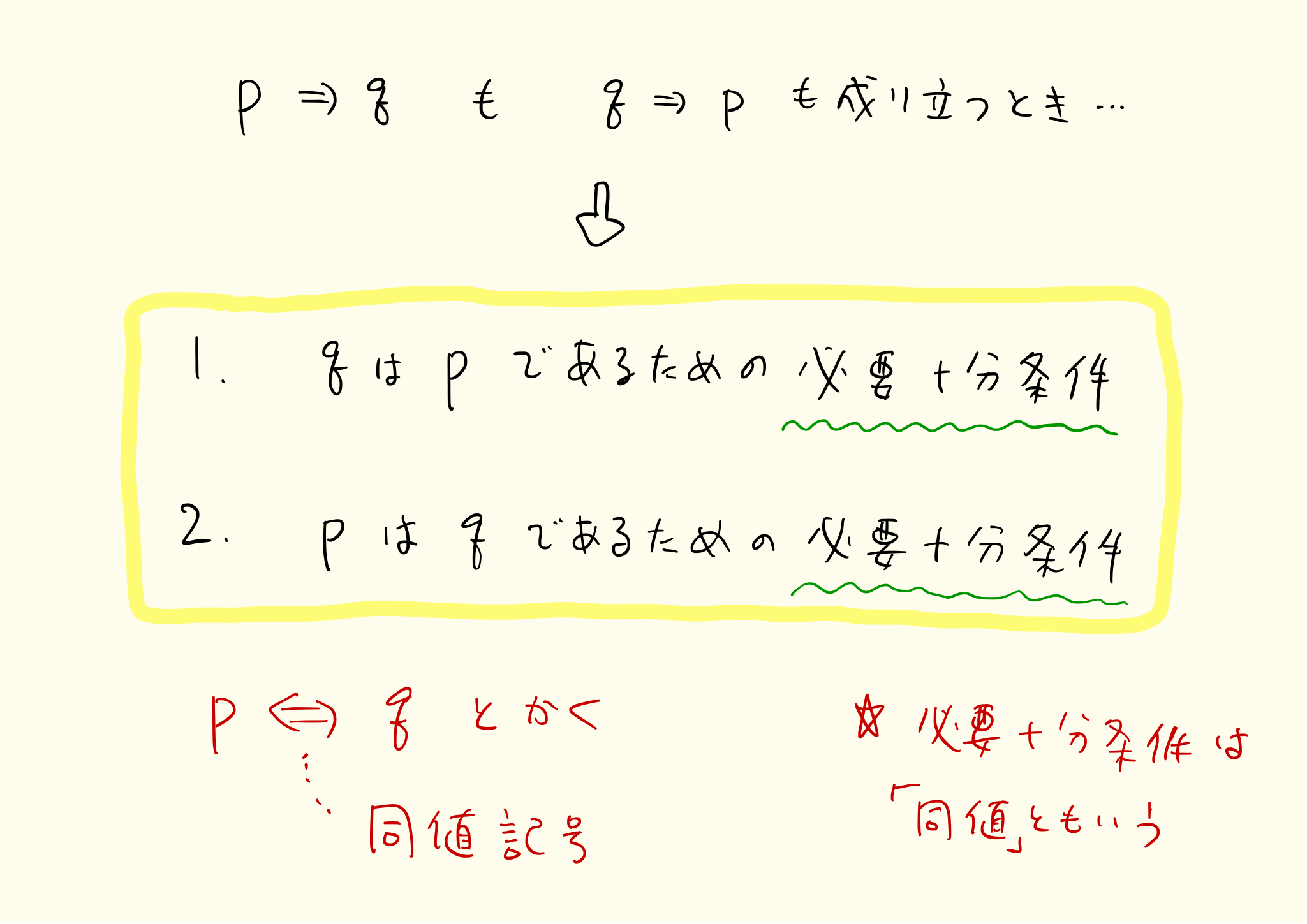
必要十分条件は同値ともいいます。