右手系3次元座標とベクトルの外積の定義と公式

$3$ 次元座標には右手系と左手系がある。右手の親指と人差し指と中指を互いに直交するように開いて、親指を $x$ 軸、人差し指を $y$ 軸、中指を $z$ 軸にしたような座標を右手系という。また親指と人差し指はそのままで中指と真逆の向きを $z$ 軸にしたような座標を左手系という。

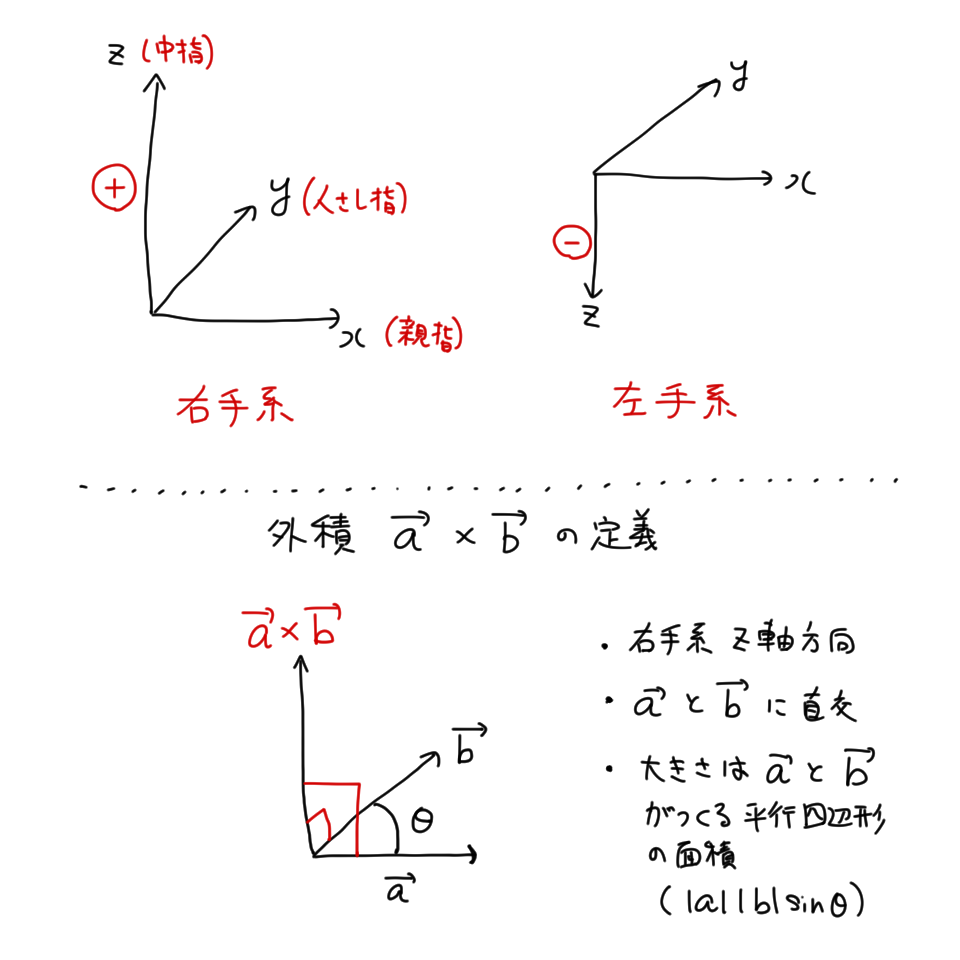
ベクトルの外積を考えるときは右手系の座標を使う。

外積の定義

ベクトル $\mathbf{a},\ \mathbf{b}$ の外積 $\mathbf{a}\times\mathbf{b}$ を次のように定義する。

外積の定義

\[ (1)\ \ \mathbf{a}\times\mathbf{b}=(|\mathbf{a}||\mathbf{b}|\sin\theta)\ \mathbf{e}\\ (2)\ \ \mathbf{0}\times\mathbf{a}=\mathbf{a}\times\mathbf{0}=\mathbf{0} \]

ここでベクトル $e$ は $\mathbf{a}$ と $\mathbf{b}$ を右手系 $3$ 次元座標の $x$ 軸と $y$ 軸に置いたときの $z$ 軸方向の単位ベクトルで、 $\mathbf{a}$ と $\mathbf{b}$ に直交しているとする。

また $\theta$ を $\mathbf{a}$ と $\mathbf{b}$ のなす角とする。

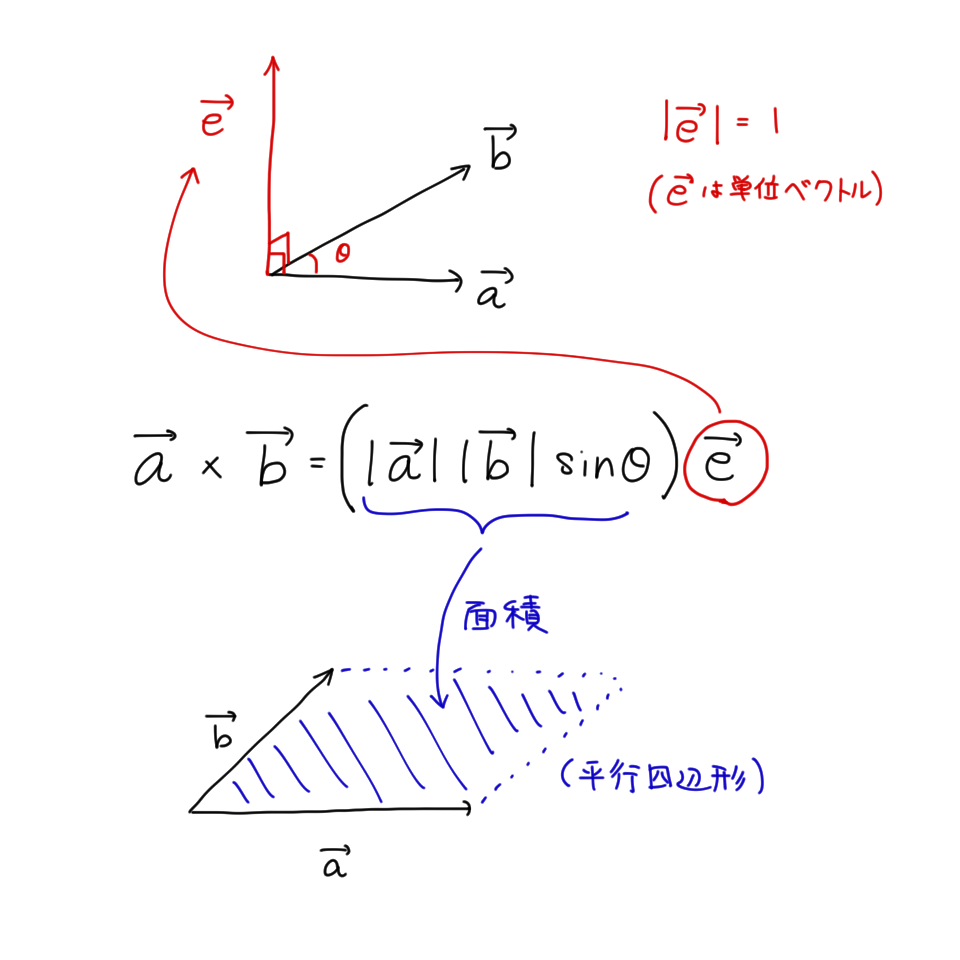
外積の大きさはベクトル $\mathbf{a}$ と $\mathbf{b}$ がなす平行四辺形の面積になっている。

また零ベクトル $\mathbf{0}$ と任意のベクトルの外積を零ベクトル $\mathbf{0}$ とする。零ベクトルの外積は定義 $(1)$ からも導かれるが、特に重要であるため定義に入れた。

外積の公式

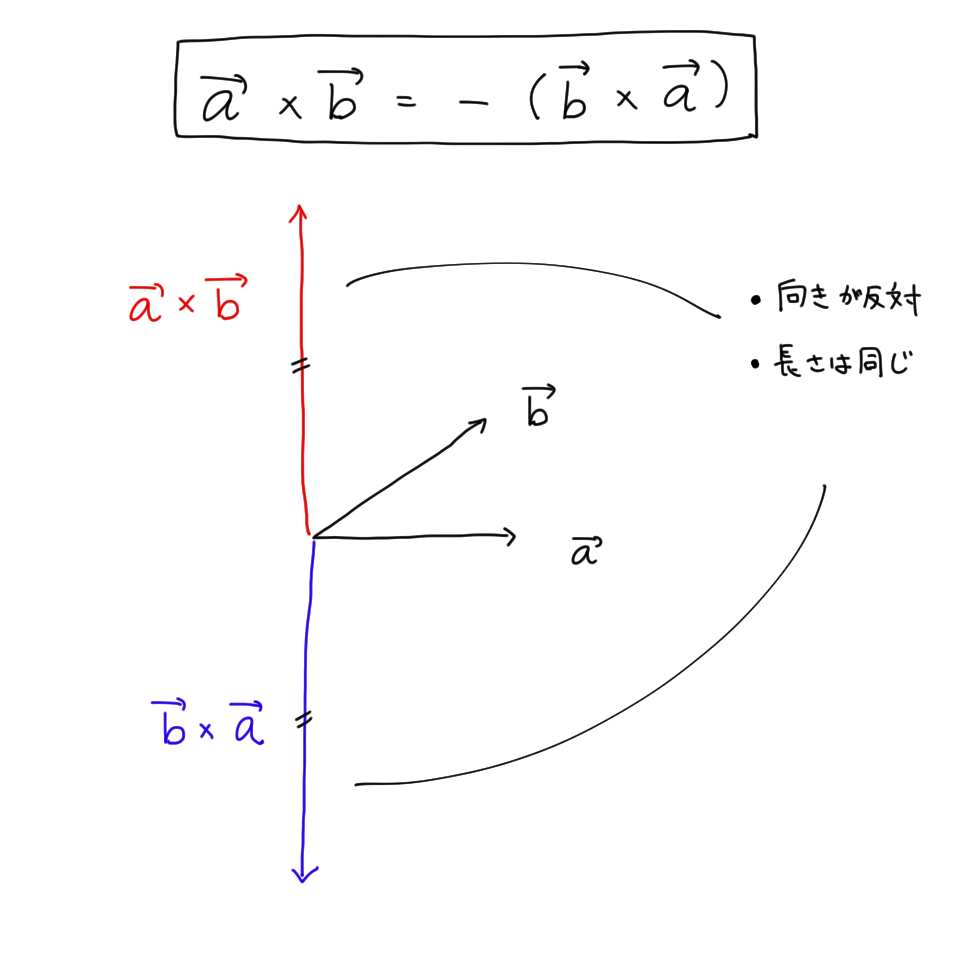
ある意味、外積は内積と反対の概念である。それは次の公式からわかる。

外積の公式

ベクトル $\mathbf{a},\ \mathbf{b},\ \mathbf{c}$ と実数 $m$ について

\[ (1)\ \ \mathbf{a}\times\mathbf{b}=-\mathbf{b}\times\mathbf{a}\\ (2)\ \ (m\mathbf{a})\times\mathbf{b}=\mathbf{a}\times(m\mathbf{b})=m(\mathbf{a}\times\mathbf{b})\\ (3)\ \ (\mathbf{a}\times\mathbf{b})\times\mathbf{c}=\mathbf{a}\times\mathbf{c}+\mathbf{b}\times\mathbf{c}\\ (4)\ \ \mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})=\mathbf{b}\cdot(\mathbf{c}\times\mathbf{a})=\mathbf{c}\cdot(\mathbf{a}\times\mathbf{b}) \]

が成り立つ。ただし最後の式のドットはベクトルの内積を意味する。