LaTeXコマンド 微分と偏微分のさまざまな記号(導関数に値を代入する記法など)
微分は f'(x) のように関数にダッシュをつけたり、df/dx のように分数で表したり、いろいろな記法がある。
微分(分数を使わない方法)
\dot{x}
\ddot{x}
x^{\prime}
x^{\prime\prime}
f' (x)
f^{\prime}(x)
f^{\prime\prime}(x)
f^{\prime\prime\prime}(x)
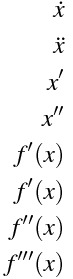
ダッシュを使うときは、ダッシュの後に半角空白を入力する。半角空白を入れないとダッシュが正しく表示されない。
ダッシュコマンドでは二次導関数以上のダッシュが表示されないため、基本的にダッシュではなく prime コマンドを使う。prime であればいくらでも追加できる。
変数の上にドットという表記は特に物理で使われる。ドットが一個で一階微分、ドットが二個で二階微分。
微分(分数を使う方法)
\frac{df}{dx}
\frac{d}{dx}f
\frac{d^2 f}{dx^2}
\frac{d^2}{dx^2}f
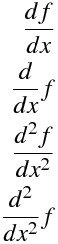
導関数のdをイタリック体にしたくないときは次のようにする。
\frac{\mathrm{d}f}{\mathrm{d}x}
\frac{\mathrm{d}}{\mathrm{d}x}f
\frac{\mathrm{d}^2 f}{\mathrm{d}x^2}
\frac{\mathrm{d}^2}{\mathrm{d}x^2}f
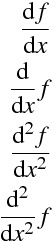
導関数に値を代入する
\frac{df}{dx}(1)
\frac{df}{dx}|_{x=1}
\left.\frac{df}{dx}\right|_{x=1}
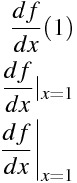
| を伸ばすためにはleftとrightのコマンドを使うが、| は一本しかない。left の後の | を省略するためにはドットを書く。もしleftを書かないとエラーが出る。
偏微分のいろいろな記法
f_{x}
f_x
f_{xy}
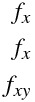
partial を使うと 6 を反対にしたような記号が表示される。
\partial_{x} f
\frac{\partial f}{\partial x}
\frac{\partial{f}}{\partial{x}}
\frac{\partial}{\partial x}f
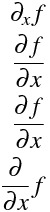
n次導関数
f^{(2)}(x)
f^{(3)}(x)
f^{(n)}(x)
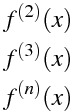
ラプラシアンとナブラ
\Delta = \nabla^2
\Delta = \sum_{k=1}^{n} \frac{\partial^{2}}{\partial x_{k}^{2}}
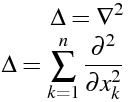
記号・文字

-
 TeX(LaTeX)で単位をきれいに書く方法
TeX(LaTeX)で単位をきれいに書く方法0
7557
-

-
 LaTeX(MathJax)の矢印コマンド一覧
LaTeX(MathJax)の矢印コマンド一覧0
1489
-
 LaTeX数式コマンド一覧
LaTeX数式コマンド一覧0
5895
-

-
 三角形と合同の記号をTeX(LaTeX)で書くコマンド
三角形と合同の記号をTeX(LaTeX)で書くコマンド0
22521
-
 プラスマイナスの記号をTeX(LaTeX)で書く
プラスマイナスの記号をTeX(LaTeX)で書く0
44645
-
 LaTeX で自然数、整数、有理数、実数、複素数の集合を表す
LaTeX で自然数、整数、有理数、実数、複素数の集合を表す0
57287
-
 論理記号(否定、論理積、同値、∀、∃)をTeXで書く方法
論理記号(否定、論理積、同値、∀、∃)をTeXで書く方法0
14502
-

-
 LaTeXコマンド ベクトルの記号
LaTeXコマンド ベクトルの記号0
7005
-

-
 LaTeXコマンド 角度(度数法と弧度法と記号)
LaTeXコマンド 角度(度数法と弧度法と記号)0
3319
-

-

-

-
 LaTeXコマンド:積分と重積分
LaTeXコマンド:積分と重積分0
1433
-
 LaTeX記法 分数とカッコの使い方
LaTeX記法 分数とカッコの使い方0
2729
-

-
 LaTeX記法 集合(包含関係と和集合とsup)
LaTeX記法 集合(包含関係と和集合とsup)0
52019
-
 絶対値(ノルム)記号|LaTeX
絶対値(ノルム)記号|LaTeX0
27715
-
 LaTeX で平方根とべき根を書く
LaTeX で平方根とべき根を書く0
3295
-
 LaTeXコマンド:等号や不等号などの記号
LaTeXコマンド:等号や不等号などの記号0
23826




