東大数学科卒が高校数学の効率的な勉強法をわかりやすく解説します：解ける問題は最後まで解かない

高校数学を得意にして成績を伸ばす方法をわかりやすく解説します。はじめに数学が苦手な人、得意な人に向けて大雑把な注意点をあげます。

• 数学が苦手な人は図を意識する
• 数学が得意な人は計算を意識する

数学が苦手な人は図を意識しよう

数学を苦手から得意にするには図とグラフを使いこなす必要があります。

小学校で習うかけ算の分配法則は、計算の方法とみるか、長方形の分割と考えるかで見方が変わりますね。このように数学は式と図形の二面性をもちますが、数学が苦手な方は図形の側面を見ていないことが多い。

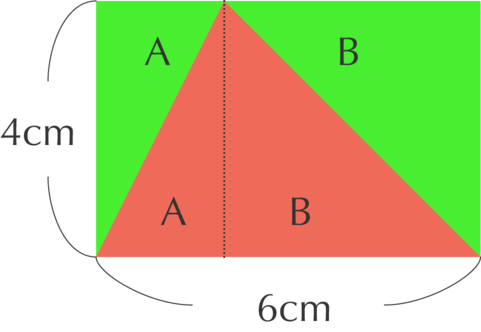
抽象的な表現ですが、数学が苦手な人は「図形をとにかく描く」勉強を試そう。例えば次の図をきちんと描いてください。

• 二次関数のグラフ
• 円周角の定理や正弦定理で出てくる図
• ベクトルの図

定規を使わずにきれいな図を描くことは数学力の向上につながります！

数学が得意な人は計算を意識しよう

数学が得意な人がさらに数学を得意にするためにはどうすればいいでしょうか。

それは計算力を上げることです。大学受験の数学（特に微分積分）は複雑な計算をたくさん要求する。上位層からさらに上に抜き出るためには計算力を上げるしかない。慶應医学部などの私大医学部を目指す人は特に必須です。

計算は微分積分や三角関数の計算だけではありません。小学校レベルのかけ算や割り算、中学校レベルの連立方程式も含みます。計算力を上げると化学の試験でも有利になりますよ。

そして暗算を意識しよう。暗算ができる人は高速に計算します。教科書の例題を頭の中で解いたり、二桁のかけ算を暗算で計算したりしてみよう。三角関数の公式を加法定理から導くとか。暗算すると計算ミスが減るの記事はぜひ読んでください。

平方数などの基本的な計算は暗記してください。受験で暗記すべき計算も確認してくださいね。

数学が苦手な新高校一年生に向けた勉強法

高校では二次関数を始めに習いますが、実は二次関数はとても難しく、多くの人がここでつまづいてしまう。二次関数でつまづいて数学を嫌いになるパターンはとても多い。

二次関数を無事クリアしても、その後の三角比でつまづく可能性があります。

高校一年生がつまづきやすい分野は二次関数と三角比の二つ。ここをクリアできれば OK ですが、この二つはまったく正反対の勉強法が必要です。

• 二次関数は深く考えず、問題をたくさん解く
• 三角比は深く考えて、問題は少し解く

教科書や問題集の解説はどちらもある程度読まないといけませんが、二次関数は解説をそれほど丁寧に読まなくてもだいじょうぶ。ちなみに二次関数は平方完成の理解にかかっているので、平方完成は絶対にマスターしてくださいね。

二次関数は一問一問に深く入りこむと効率が悪くなり、進度が遅くなります。スポーツをやっているような気分で、なにも考えず問題に当たって砕けてをくりかえすとコツがわかってくるでしょう。

一方、三角比は二次関数と比べて量も質もボリュームがなく、落ち着いて考えればわかってくる分野です。授業で習うサインやコサインの定義をきちんと理解すれば、問題をたくさん解かなくても三角比はマスターできます。三角比の公式も覚えることはほとんどありません。

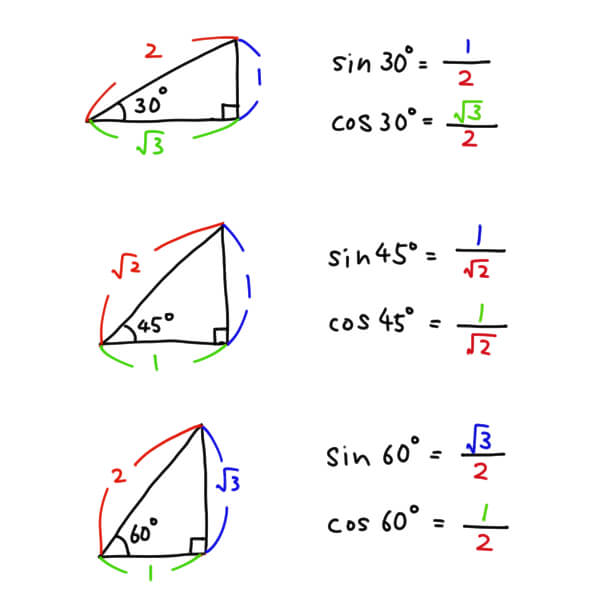
参考書と問題集は基本的に学校から配布される教科書とワークを使ってください。むやみに市販の教材に手を伸ばすと効率が落ちます。特にワークは二次関数をマスターできるだけの問題をもっており、新高校一年生にとって最適な教材といえます。

数学は教科書や問題集を変えても伸びない。自分を変えることで伸びる。教科書とワークと一年間向き合い、その中で自分を変えていく必要があるでしょう。

数学が苦手な新高校二年生に向けた勉強法

高校二年生の数学は微分積分やベクトルといった難しい分野が目白押しで、高校生にとってはターニングポイントになるでしょう。今まで数学が得意だった人も勉強を怠ると一気に転落するため、毎日必ず勉強してください。

数ⅡBは一年生に勉強したことを使います。例えば数ⅡBで一番やっかいな三角関数は三角比を使い、微分積分は二次関数を使う。一年生で習った知識が身についていないとかなりきつい。わからない問題が出てきたら、原因が数ⅠAにないか考えてみよう。

そして一番の問題は癖です。数ⅡBは数ⅠAより癖が強く、好き嫌いがはっきりしてくる。数学が嫌いな人はもっと嫌いに、好きな人はもっと好きになる傾向にあります。

嫌いな人がもっと嫌いになる理由はベクトルといった新しい分野のわかりづらさにあります。二年生になったら自分に合ったわかりやすい参考書を探すことがなにより重要になるでしょう。自分に合わない教材を選ぶと膨大な時間をロスします。

二年生は文理の選択と受験する大学と学部をそろそろ決める時期。大学・学部によっては数学が不要という場合もあり、「数学をどのように勉強するか」の前に「自分は将来どうしたいか？」を考えてください。その上で数学の勉強方針を変更しましょう。

文系私大を目指すと決めたら数学はそれほど一生懸命になる必要はなく、医学部を目指すと決めたら今の何倍もこれから勉強しないといけません。これまでをまとめてみましょう。

• 毎日勉強する
• 数ⅠAはきちんとおさえる
• 自分に合った参考書・問題集を慎重に探す
• 将来を考えつつ数学の勉強方針は適宜変更する
• 苦手ポイントは別個に対応する（後述）

数学が苦手な新二年生におすすめの参考書と問題集

まずは高校数学でおすすめの参考書を読んでください。

参考書は合う合わないがありますが、学研の「数学Ⅱをひとつひとつわかりやすく」はかなりおすすめ。本書は数学が苦手な人を対象として、デザインがやさしいタッチでとっつきやすい。最初は教科書で勉強し、わからない問題が出てきたら本書を使うといいでしょう。参考書としてあげていますが、問題集にもなります。

肝心の問題集ですが、みんなが使うという理由でチャート式は使わないでください。

自分に合う合わないをはっきりさせて使う分にはいいですが、少しでも合わないと思ったら使わない。チャート式は分厚いため、数学が苦手な人は「勉強しても勉強しても終わらない」という無用なストレスを抱える傾向にあります。どれを使うか迷ったらワーク（教科書に沿った問題集）だけでいい。

数ⅡBで苦手になりやすい分野

• 軌跡
• 三角関数

実は多くの二年生は微分積分ではあまりつまづかない。数学といえば微分積分。だから一生懸命勉強しないと、と最初から身構えて勉強するからかもしれません。

積分はつまるところ面積の計算なので、慣れてくると簡単に感じるでしょう。

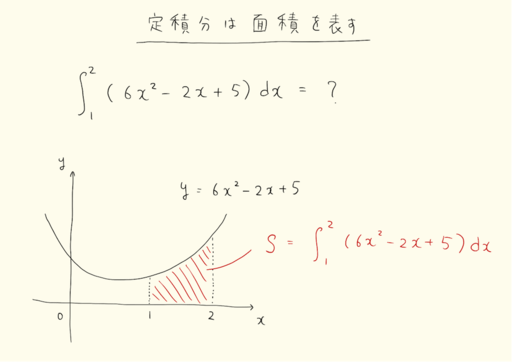
数ⅡBは微分積分よりも軌跡と三角関数に気をつけよう。この二つは本当に難しい。

軌跡は「図形と方程式」の小分野で、普通の学校では一学期期末試験の範囲になるでしょう。軌跡は決定的に差がつきます。勉強してもなんだかわからないという人がたくさんいます。

そして三角関数。三角関数は軌跡と違って、それ自体が大きな分野で、二学期中間試験はおそらく丸ごと三角関数です。油断すると一学期と二学期で点が大きく変わるでしょう。三角関数は覚えることがやたら多く、癖がとても強い。三角比のサインコサインの計算に抵抗があるとものすごく苦戦する。三角関数の勉強法がたくさん読まれているのもうなずけます。

軌跡と三角関数の勉強法

場合によりますが、軌跡はひとまず無視しよう。範囲の関係から軌跡をそれほど出題しないという学校や先生もいます。

軌跡をどうにか理解したい人は、二次関数と同様に「なぜ？」という疑問を捨てて、問題をたくさん解いて解法のパターンを覚えてください。アポロニウスの円など典型的な問題を同じやり方で解いて「こんなものかな～」とわかったふりをする。数学なんてわかったふりですよ、つまるところ。

同じような問題を解いていると「これはこういうことなのかな」と本質がだんだんわかってきます。最初から本質を探るよりも効率がいいはずです。

三角関数は公式の覚え方で効率が変わります。学校の定期試験の難しさによりますが、次の公式だけを覚えてください。

• 加法定理（sin、cos、tan）
• 倍角の公式（sin、cos、tan）
• 合成の方法（公式ではないが、やり方は絶対に覚える）

三角関数は公式がたくさんありますね。勉強法を知らないとすべて覚えようとしますが、その必要はありません。加法定理、倍角の公式、そして三角関数の合成だけで足ります。

半角の公式、積和・和積公式はすべて加法定理をもとに自分で証明してみよう。三角関数の公式はすべて根っこに加法定理があるので、究極のところ加法定理さえ覚えていればなんとかなってしまう（だからといって加法定理だけ覚えればいい…というのはダメ）。

最初は和積公式の一つ一つを 1 分以内に導くように訓練してください。三角関数の定期試験はこれをどれだけやったかで点が変わります。逆に考えると、公式を組み立てる訓練さえきちんとやれば、三角関数はマスターできてしまう。

加法定理を使って公式を導くという面倒なステップを踏まないと、いつまでも三角関数はできるようにならない。

数学が苦手な新高校三年生に向けた勉強法（数Ⅲの勉強法）

数Ⅲは高校数学で最も難しく、最も時間がかかる。効率よくスピード感をもって勉強することを意識し、参考書と問題集の選択に注意しよう。

大学受験の準備もあるため、数Ⅲは秋頃までにマスターするようにします。

数Ⅲはチャート式数学を用いた数Ⅲ微分積分の最短勉強法にあるように、まず計算問題だけを勉強し、数Ⅲの大枠をつかむと楽です。教科書どおりに勉強してもなかなかスムーズにいかない人は、そういった状態が当たり前だと気を楽にして、計算だけは解けるようにしてください。

数Ⅲほど計算が重要な分野はありません。不思議なことに、計算ができるようになると他の問題もできるようになる。

数学が嫌いでどうしようもない方へ

数学が苦手を超えて嫌いになっている人は無理して数学を勉強することはありません。数学を使わない大学を受験すればいいことです。

定期テストは努力と根性で乗りきるしかありませんが、大嫌いなピーマンをどうにか食べるように、大嫌いな数学をどうにか乗りきることで精神的な成長も（たぶん）あるはず。

定期テストでそこそこいい点をとるためには、どうしてもわからない小分野をばっさり捨てることがポイント。高校生におすすめの本で解説しているように、勝つために負けることが大切です。

「俺は完璧主義者だ。全部理解しないと気がすまない」

という人はその性格を捨てよう。数学は「このくらいでいいや～軌跡はわかったふりでいいや～」という大胆な判断が必要です。

すべての分野を等しくやっつけようとすると、数学への嫌悪感が増して効率が落ちます。最初から六割とれればいいという心構えで挑み、四割を最初から捨ててしまう。するとその六割は確実にとろうと努力するはずです。

参考 学校の先生が教えない「選択と集中」

数学が得意な高校生に向けた勉強法

冒頭で述べたように、数学の得意な人がもっと得意になるためには計算力が必要です。

高校生は受験と定期試験の両方を対策しないといけませんが、定期試験の対策は（そこそこ）受験対策につながります。期末試験を疎かにして勝手に勉強するというやり方は間違っています。数学はすべての問題に深い意味が隠れている学問で、定期試験の対策が受験につながらないということはない。

しかし学校の進度が遅い、自分の目指している大学のレベルとかけ離れている場合は、学校の勉強は授業で完結させて、それ以外の時間は自分の勉強をするというメリハリが必要になるでしょう。学校の休憩時間に次の授業の復習や予習をすませるという勉強法をおすすめします。

授業中も先生の講義を聞きながら前回の復習をしてみるといいですね。休み時間や授業時間のこうした習慣は積もりに積もって成果に表れるはず！

数学の勉強効率を上げる方法

数学を最後まで解かないという方針をとった人とそうでない人では勉強の効率に大きな差が生まれます。

多くの人は数学を最後まで解く。答えをきちんと出すまでその問題に向き合っている。たとえやり方がわかって、あとは面倒な計算を経て答えを出すだけとわかったとしても、最後の最後まで解く。

理論を固めていく段階（高校二年生まで）は、最後まで計算して解くよりも、理論を理解して問題の癖を覚えるほうに時間をかけてください。問題のたびに最後まで計算するという方法は高校三年生になってからで間に合います。

高校二年生まではわかりきった問題をねちねち解かない。たいていは自己満足です。

やり方がわかった瞬間、その問題はほぼ攻略したも同然。それでも答えを出すためにねちねちねちねち計算し続けるのは多くの場合自己満足で、そこに数学的な成長はあまりない。きれいなノートは自己満足といった記事でくりかえし解説していますが、多くの人はさまざまな自己満足にとらわれて時間を浪費しています。

模試を思い出してください。「やり方はわかった。後は計算だけ！」という状態になったら安心しませんか？　安心するのは、解法がわかった時点で残りは作業でしかないとあなた自身がわかっているからです。それにもかかわらず多くの受験生は「作業でしかない残り」に莫大な時間を注いでしまう。数学的な能力が一番試されるのは解法を見つけるときだとわかっていながら、解法を見つけるための勉強時間は増やそうとしない。数学を勉強しても伸びない最大の原因はここにあります。

• 頭を使わない残り作業に大量の時間を費やしている
• 頭を使う勉強に時間を費やしていない

という勉強は今すぐやめてください。

計算問題を除いて 1 時間で何問解きますか？　2～4 問だったら少し量が足りない。1 時間で 3 問くらいだと、1 日 10 問くらいが限界。しかし数学の力を本当につけたいのなら、1 日に 20 問解くくらいでないといけない。

くりかえしになりますが、頭を使う作業と頭を使わない作業を明確に区別し、頭を使わない作業時間を極限まで減らしてください。これがうまくできるようになると数学の勉強効率は飛躍的に向上します。

参考
計算ミスを 90% 以上減らす方法
受験勉強とノート
大学受験生の直前期の勉強法
東大に合格する方法